题目内容
△ABC中，若
+
=
，则B= ．
| 1 |
| a+b |
| 1 |
| b+c |
| 3 |
| a+b+c |
考点：余弦定理
专题：计算题,解三角形
分析：将已知条件化简整理，得到c2+a2=ac+b2，再由余弦定理，即可得到角B．
解答：
解：若
+
=
，
则
+
=3，
即有
+
=1，
即为bc+c2+a2+ab=ab+ac+b2+bc，
即有c2+a2=ac+b2，
由余弦定理可得，cosB=
=
=
，
由于0＜B＜π，则B=
．
故答案为：
．
| 1 |
| a+b |
| 1 |
| b+c |
| 3 |
| a+b+c |
则
| a+b+c |
| a+b |
| a+b+c |
| b+c |
即有
| c |
| a+b |
| a |
| b+c |
即为bc+c2+a2+ab=ab+ac+b2+bc，
即有c2+a2=ac+b2，
由余弦定理可得，cosB=
| a2+c2-b2 |
| 2ac |
| ac+b2-b2 |
| 2ac |
| 1 |
| 2 |
由于0＜B＜π，则B=
| π |
| 3 |
故答案为：
| π |
| 3 |
点评：本题考查余弦定理的运用，考查代数式的化简变形的运算能力，属于基础题．
练习册系列答案
相关题目
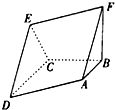如图空间几何体ABCDEF中，四边形ADEF为平行四边形，FB⊥平面ABCD，AB∥CD，AB⊥BC，AB=BC=