题目内容
记集合A={（x，y）|x2+y2≤4}和集合B={（x，y）|x+y-2≤0，x≥0，y≥0}表示的平面区域分别为Ω1，Ω2．若在区域Ω1内任取一点M（x，y）．则点M落在区域Ω2的概率为 ．
考点：几何概型
专题：概率与统计
分析：求出平面区域Ω1，Ω2的面积，利用几何槪型的概率公式即可得到结论．
解答：
.解：作出不等式组对应的：平面区域如图：
则集合A对应区域Ω1的面积S1=π×22=4π，
集合B对应的区域Ω2为直角三角形OAB，对应的面积S2=
×2×2=2，
则若在区域Ω1内任取一点M（x，y）．则点M落在区域Ω2的概率P
=
=
，
故答案为：
则集合A对应区域Ω1的面积S1=π×22=4π，
集合B对应的区域Ω2为直角三角形OAB，对应的面积S2=
| 1 |
| 2 |
则若在区域Ω1内任取一点M（x，y）．则点M落在区域Ω2的概率P
| S2 |
| S1 |
| 2 |
| 4π |
| 1 |
| 2π |
故答案为：
| 1 |
| 2π |
点评：本题主要考查几何槪型的概率的计算，利用数形结合求出对应区域的面积是解决本题的关键．
练习册系列答案
同步练习强化拓展系列答案
相关题目
已知i是虚数单位，若
=2+i（a，b∈R），则复数a+bi在复平面内对应的点位于（ ）
| 1-i |
| a+bi |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
已知a=log23，b=ln2，c=5 -
，则a，b，c的大小关系是（ ）
| 1 |
| 2 |
| A、a＞c＞b |
| B、a＞b＞c |
| C、b＞a＞c |
| D、b＞c＞a |
已知sin（α-
）=
，则cos（
+α）的值为（ ）
| π |
| 6 |
| 1 |
| 3 |
| π |
| 3 |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
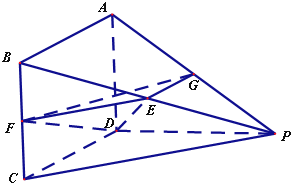如图，在四棱锥P-ABCD中，四边形ABCD是正方形，CD=PD，∠ADP=90°，∠CDP=120°，E，F，G分别为PB，BC，AP的中点．
