题目内容
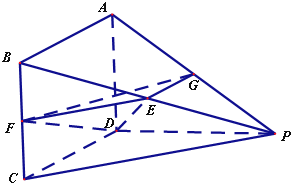 如图,在四棱锥P-ABCD中,四边形ABCD是正方形,CD=PD,∠ADP=90°,∠CDP=120°,E,F,G分别为PB,BC,AP的中点.
如图,在四棱锥P-ABCD中,四边形ABCD是正方形,CD=PD,∠ADP=90°,∠CDP=120°,E,F,G分别为PB,BC,AP的中点.(Ⅰ)求证:平面EFG∥平面PCD;
(Ⅱ)求二面角D-EF-B的平面角的大小.
考点:与二面角有关的立体几何综合题,平面与平面平行的判定
专题:综合题,空间位置关系与距离,空间角
分析:(Ⅰ)欲证平面EFG∥平面PCD,可根据面面平行的判定定理进行证明,即证明EG∥平面PCD,EF∥平面PCD;
(Ⅱ)取PC中点M,连接EM,DM,根据二面角的平面角的定义证明∠DEM就是二面角D-EF-B的平面角的补角,在△DEM中,即可求出二面角B-EF-D的平面角的大小.
(Ⅱ)取PC中点M,连接EM,DM,根据二面角的平面角的定义证明∠DEM就是二面角D-EF-B的平面角的补角,在△DEM中,即可求出二面角B-EF-D的平面角的大小.
解答:
 (Ⅰ)证明:因为E,G分别为BP,AP中点,
(Ⅰ)证明:因为E,G分别为BP,AP中点,
所以EG∥AB,
又因为ABCD是正方形,AB∥CD,所以EG∥CD,
所以EG∥平面PCD.
因为E,F分别为BP,BC中点,所以EF∥PC,
所以EF∥平面PCD.
所以平面EFG∥平面PCD.
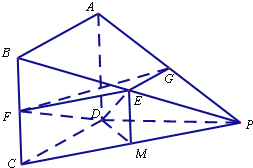
(Ⅱ)解:取PC中点M,连接EM,DM,则EM∥BC,
又AD⊥平面PCD,AD∥BC,所以BC⊥平面PCD,
所以EM⊥平面PCD,所以EM⊥DM,EM⊥PC.
因为CD=DP,则DM⊥PC,所以 DM⊥平面PCB.
又因为EF∥PC,所以EF⊥EM,
所以∠DEM就是二面角D-EF-B的平面角的补角.
不妨设AD=CD=PD=2,则EM=1,DM=1,∠DEM=
.
所以二面角D-EF-B的平面角的大小为
π.
 (Ⅰ)证明:因为E,G分别为BP,AP中点,
(Ⅰ)证明:因为E,G分别为BP,AP中点,所以EG∥AB,
又因为ABCD是正方形,AB∥CD,所以EG∥CD,
所以EG∥平面PCD.
因为E,F分别为BP,BC中点,所以EF∥PC,
所以EF∥平面PCD.
所以平面EFG∥平面PCD.
(Ⅱ)解:取PC中点M,连接EM,DM,则EM∥BC,
又AD⊥平面PCD,AD∥BC,所以BC⊥平面PCD,
所以EM⊥平面PCD,所以EM⊥DM,EM⊥PC.
因为CD=DP,则DM⊥PC,所以 DM⊥平面PCB.
又因为EF∥PC,所以EF⊥EM,
所以∠DEM就是二面角D-EF-B的平面角的补角.
不妨设AD=CD=PD=2,则EM=1,DM=1,∠DEM=
| π |
| 4 |
所以二面角D-EF-B的平面角的大小为
| 3 |
| 4 |
点评:本题主要考查了平面与平面平行的判定,以及与二面角有关的立体几何综合题,考查学生空间想象能力,逻辑思维能力,是中档题.

练习册系列答案
相关题目
记等比数列an的前项和为Sn,若a1=
,S2=2,则S3=( )
| 1 |
| 2 |
| A、2 | ||
| B、6 | ||
| C、16 | ||
D、
|
设i为虚数单位,则复数z=
在复平面内对应的点在( )
| i2014 |
| 1-i |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
一个等差数列共有10项,其中奇数项的和为
,偶数项的和为15,则这个数列的第6项是( )
| 25 |
| 2 |
| A、3 | B、4 | C、5 | D、6 |
若复数z满足(1+i)z=i,则复数z的虚部为( )
A、
| ||
B、
| ||
| C、1 | ||
| D、i |
