题目内容
已知函数f（x）=-sin（2x+π）+
sin（2x+
）
（1）求f（x）的对称轴方程；
（2）若将f（x）的图象向右平移
个单位，得到函数g（x）的图象，求函数g（x）在区间[0，
）上的最大值和最小值，并求出相应的x的值．
| 3 |
| π |
| 2 |
（1）求f（x）的对称轴方程；
（2）若将f（x）的图象向右平移
| π |
| 3 |
| π |
| 2 |
考点：两角和与差的正弦函数,函数y=Asin（ωx+φ）的图象变换
专题：三角函数的图像与性质
分析：（1）利用诱导公式和两角和公式对函数解析式化简，根据三角函数图象求得函数的对称轴方程．
（2）利用三角函数图象的变换求得g（x）的解析式，继而根据x的范围求得函数的最大值和最小值．
（2）利用三角函数图象的变换求得g（x）的解析式，继而根据x的范围求得函数的最大值和最小值．
解答：
解：（1）f（x）=-sin（2x+π）+
sin（2x+
）
=sin2x+
cos2x
=2sin（2x+
），
令2x+
=kπ+
，得到函数对称轴方程为x=
+
（k∈Z）．
（2）∵将f（x）的图象向右平移
个单位，得到函数g（x）的图象，
∴g（x）=f（x-
）=2sin[2（x-
）+
]=2sin（2x-
）．
∵x∈[0，
）时，2x-
∈[-
，
），
∴当2x-
=
，即x=
时，g（x）取得最大值2；
当2x-
=-
，即x=0时，g（x）取得最小值-
．
| 3 |
| π |
| 2 |
=sin2x+
| 3 |
=2sin（2x+
| π |
| 3 |
令2x+
| π |
| 3 |
| π |
| 2 |
| kπ |
| 2 |
| π |
| 12 |
（2）∵将f（x）的图象向右平移
| π |
| 3 |
∴g（x）=f（x-
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
∵x∈[0，
| π |
| 2 |
| π |
| 3 |
| π |
| 3 |
| 2π |
| 3 |
∴当2x-
| π |
| 3 |
| π |
| 2 |
| 5π |
| 12 |
当2x-
| π |
| 3 |
| π |
| 3 |
| 3 |
点评：本题主要考查了三角函数恒等变换的应用，三角函数图形和性质，三角函数图象的变换等知识．综合考查了学生对基础知识的理解和掌握．
练习册系列答案
七星图书口算速算天天练系列答案
初中学业考试导与练系列答案
相关题目
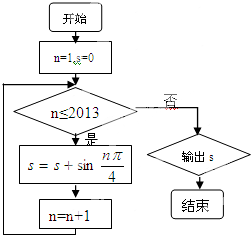
一个算法的程序框图如图，则其输出结果是（ ）
| A、0 | ||||
B、
| ||||
C、
| ||||
D、
|
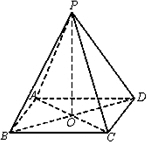如图，在四棱锥P-ABCD中，底面ABCD是矩形，四条侧棱长均相等且BD交AC于点O．