题目内容
已知数列{an}的前n项和为Sn,其中a1=1,Sn+1=2Sn+1,(n∈N*)
(1)求数列{an}的通项公式;
(2)设数列{
}的前n项和为Tn,求满足不等式Tn<
的n值.
(1)求数列{an}的通项公式;
(2)设数列{
| 1 |
| an |
| 9 |
| Sn+1 |
考点:数列的求和
专题:等差数列与等比数列
分析:(1)根据Sn+1=2Sn+1,求得Sn=2Sn-1+1两式相减求得an+1=2an,判断出{an}是一个等比数列.进而根据首项和公比求得数列的通项公式,
(2)根据等比数列的求和公式求得前n项的和,解不等式即可求出n的值.
(2)根据等比数列的求和公式求得前n项的和,解不等式即可求出n的值.
解答:
解:(1)∵Sn+1=2Sn+1,
∴n≥2时,Sn=2Sn-1+1,
二式相减得:Sn+1-Sn=2Sn-2Sn-1
∴an+1=2an,即
=2,即{an}是一个等比数列.q=2,a1=1
那么an=1×2n-1=2n-1.
(2)Sn=
═2n-1,
=
=(
)n-1,
则数列{
}是首项为1,公比q=
的等比数列,
则数列{
}的前n项和为Tn=
=2-(
)n-1,
则不等式Tn<
等价为2-(
)n-1<
,
即
•(
)n-1+(
)n-1=
•(
)n-1>2,
即(
)n-1>
,
则当n=1时,1>
,成立,
当n=2时,
>
,成立,
当n=3时,
>
,不成立,
故满足不等式Tn<
的n值为1或2.
∴n≥2时,Sn=2Sn-1+1,
二式相减得:Sn+1-Sn=2Sn-2Sn-1
∴an+1=2an,即
| an+1 |
| an |
那么an=1×2n-1=2n-1.
(2)Sn=
| 1-2n |
| 1-2 |
| 1 |
| an |
| 1 |
| 2n-1 |
| 1 |
| 2 |
则数列{
| 1 |
| an |
| 1 |
| 2 |
则数列{
| 1 |
| an |
1-(
| ||
1-
|
| 1 |
| 2 |
则不等式Tn<
| 9 |
| Sn+1 |
| 1 |
| 2 |
| 9 |
| 2n |
即
| 9 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 11 |
| 2 |
| 1 |
| 2 |
即(
| 1 |
| 2 |
| 4 |
| 11 |
则当n=1时,1>
| 4 |
| 11 |
当n=2时,
| 1 |
| 2 |
| 4 |
| 11 |
当n=3时,
| 1 |
| 4 |
| 4 |
| 11 |
故满足不等式Tn<
| 9 |
| Sn+1 |
点评:本题主要考查了数列的递推式.常需要借助数列的递推式把数列转化成等差或等比数列来解决问题.

练习册系列答案
相关题目
根据下列情况,判断三角形解的情况,其中正确的是( )
| A、a=8,b=16,A=30°,有两解 |
| B、b=18,c=20,B=60°,有一解 |
| C、a=5,c=2,A=90°,无解 |
| D、a=30,b=25,A=150°,有一解 |
在△ABC中,角A=30°,B=60°,则b:c=( )
| A、1:2 | ||
| B、2:3 | ||
C、1:
| ||
D、
|
 选修4.1:几何证明选讲
选修4.1:几何证明选讲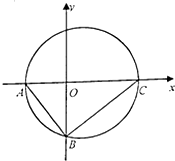 如图所示,在Rt△ABC中,已知A(-2,0),直角顶点B(0,-2
如图所示,在Rt△ABC中,已知A(-2,0),直角顶点B(0,-2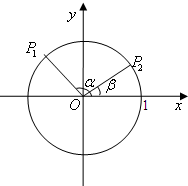 如图在单位圆中,已知α、β是坐标平面内的任意两个角,且0≤α-β≤π,
如图在单位圆中,已知α、β是坐标平面内的任意两个角,且0≤α-β≤π,