题目内容
∫
sin2xdx等于（ ）
π -π |
| A、0 | B、2π | C、4π | D、4 |
考点：定积分
专题：导数的综合应用
分析：根据函数的积分公式进行计算即可．
解答：
解：∵（-
cos2x）′=sin2x，
∴∫
sin2xdx=（-
cos2x）|
=0，
故选：A．
| 1 |
| 2 |
∴∫
π -π |
| 1 |
| 2 |
π -π |
故选：A．
点评：本题主要考查函数积分的计算，要求熟练掌握常见函数的积分公式，比较基础．
练习册系列答案
优等生题库系列答案
53天天练系列答案
相关题目
函数f（x）=x-lnx的增区间为（ ）
| A、（-∞，1） |
| B、（0，1） |
| C、（1，+∞） |
| D、（0，+∞） |
关于直线a，b，l以及平面M，N，下面命题中正确的是（ ）
| A、若a∥M，b∥M，则a∥b |
| B、若a∥M，b⊥a，则b⊥M |
| C、若a⊥M，a∥N，则M⊥N |
| D、若a?M，b?M，且l⊥a，l⊥b，则l⊥M |
下列各函数值，其中符号为负的是（ ）
| A、sin（-1000°） | ||||||
| B、cos（-2200°） | ||||||
| C、tan（-10） | ||||||
D、
|
| a |
| COSA |
| b |
| COSB |
| c |
| COSC |
| A、等腰直角三角形 |
| B、等边三角形 |
| C、顶角为120°的等腰三角形 |
| D、以上均不正确 |
若函数f（x）在x0处可导，
的值为（ ）
| lim |
| x→x0 |
| f(x0)-f(x) |
| x-x0 |
| A、f′（x0） |
| B、-f′（x0） |
| C、f′（x） |
| D、-f′（x） |
方程x3=3x-1的三根x1，x2，x3，其中x1＜x2＜x3，则x2所在的区间为（ ）
| A、（-2，-1） | ||
| B、（0，1） | ||
C、（1，
| ||
D、（
|
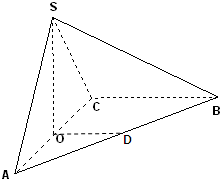在三棱锥S-ABC中，平面SAC⊥平面ABC，且△SAC是正三角形，O是AC的中点，D是AB的中点．