题目内容
设Sn为等差数列{an}的前n项和，满足S4=14，S10-S7=30．求an及Sn？
考点：等差数列的前n项和,等差数列的通项公式
专题：等差数列与等比数列
分析：利用已知条件，由等差数列的通项公式和前n项和公式列出方程组，求出首项和公差，由此能求出an及Sn．
解答：
解：∵为等差数列{an}的前n项和，
满足S4=14，S10-S7=30，
∴
，
∴
，
解得a1=2，d=1，
∴an=2+1（n-1）=n+1，
∴Sn=2n+
×1=
+
．
满足S4=14，S10-S7=30，
∴
|
∴
|
解得a1=2，d=1，
∴an=2+1（n-1）=n+1，
∴Sn=2n+
| n(n-1) |
| 2 |
| n2 |
| 2 |
| 3n |
| 2 |
点评：本题考查数列的通项公式和前n项和公式的求法，是基础题，解题时要认真审题，注意等差数列的性质的灵活运用．
练习册系列答案
相关题目
函数f（x）=ax+logax在[1，2]上的最大值和最小值之差为|a2-a|+1，则a值为（ ）
A、2或
| ||
| B、2或4 | ||
C、
| ||
| D、2 |
若函数f（x）在x0处可导，
的值为（ ）
| lim |
| x→x0 |
| f(x0)-f(x) |
| x-x0 |
| A、f′（x0） |
| B、-f′（x0） |
| C、f′（x） |
| D、-f′（x） |
如图，四棱锥A-BCDE中，底面BCDE为矩形，侧面ABC⊥底面BCDE，BC=2，CD=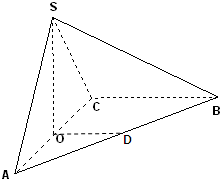
在三棱锥S-ABC中，平面SAC⊥平面ABC，且△SAC是正三角形，O是AC的中点，D是AB的中点．
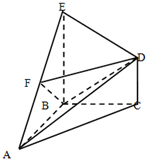如图，在几何体ABCDE中，BE⊥平面ABC，CD∥BE，△ABC是等腰直角三角形，∠ABC=90°，且BE=AB=2，CD=1，点F是AE的中点．建立适当的空间直角坐标系，利用空间向量方法解答以下问题：