题目内容
设l,m是两条不同直线,α,β是两个不同平面,则下列命题中正确的是( )
| A、若l∥α,α∩β=m,则l∥m |
| B、若l⊥α,l∥β,则α⊥β |
| C、若l∥α,m∥α,则l∥m |
| D、若l∥α,m⊥l,则m⊥α |
考点:空间中直线与平面之间的位置关系
专题:阅读型,空间位置关系与距离
分析:由线面平行的性质定理可判断A;又线面平行的性质定理和面面垂直的判定定理即可判断B;由线面平行的性质定理可判断C;由线面平行的性质定理可判断D.
解答:
解:A.若l∥α,α∩β=m,.则l,m平行或异面,只有l?β,才有l∥m.故A错;
B.若l⊥α,l∥β,则由线面平行的性质定理,l?γ,γ∩β=m,则l∥m,又l⊥α,故m⊥α,由面面垂直的判定定理得,α⊥β,故B正确;
C.若l∥α,m∥α,则由线面平行的性质可得l,m平行、相交、异面,故C错;
D.若l∥α,m⊥l,则m与α平行、相交或在平面内,故D错.
故选B.
B.若l⊥α,l∥β,则由线面平行的性质定理,l?γ,γ∩β=m,则l∥m,又l⊥α,故m⊥α,由面面垂直的判定定理得,α⊥β,故B正确;
C.若l∥α,m∥α,则由线面平行的性质可得l,m平行、相交、异面,故C错;
D.若l∥α,m⊥l,则m与α平行、相交或在平面内,故D错.
故选B.
点评:本题主要考查直线与平面平行、垂直的判定与性质定理的应用,考查空间想象能力,注意定理的条件的全面性,以及直线与平面的位置关系,是一道基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
在△ABC中,若
=1,则∠C的大小为( )
| c2-a2 |
| b2+ab |
A、
| ||
B、
| ||
C、
| ||
D、
|
如果某物体的运动方程为s=2(1-t2)(s的单位为m,t的单位为s),那么其在1.2s末的瞬时速度为( )
| A、-4.8m/s |
| B、-2.8m/s |
| C、0.88 m/s |
| D、4.8 m/s |
将函数f(x)=2sin(2x-
)的图象向左平移
个单位后,所得图象的一个对称中心是( )
| π |
| 3 |
| π |
| 6 |
A、(
| ||
B、(
| ||
C、(
| ||
D、(
|
 某四棱锥的三视图如图所示,记A为此棱锥所有棱的长度的集合,则( )
某四棱锥的三视图如图所示,记A为此棱锥所有棱的长度的集合,则( )| A、2∈A,且4∈A | ||||
B、
| ||||
C、2∈A,且2
| ||||
D、
|
若在△ABC中,有sin
=cosA,则△ABC一定是( )
| C |
| 2 |
| A、锐角三角形 |
| B、钝角三角形 |
| C、直角三角形 |
| D、等腰三角形 |
对于任意x∈[-1,0],恒有
x3-x2-3x-2m≤3成立,则m的取值范围为( )
| 1 |
| 3 |
A、[-
| ||
| B、[-1,+∞) | ||
C、[-
| ||
| D、[-2,+∞) |
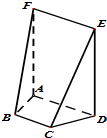 如图,在五面体ABCDEF中,四边形ADEF是正方形,FA⊥面ABCD,BC∥AD,CD=1,AD=
如图,在五面体ABCDEF中,四边形ADEF是正方形,FA⊥面ABCD,BC∥AD,CD=1,AD=