题目内容
10.已知向量,满足$\overrightarrow a•(\overrightarrow a-2\overrightarrow b)=3$,且$|\overrightarrow a|=1$,$\overrightarrow b=(1,1)$,则$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为( )| A. | $\frac{2π}{3}$ | B. | $\frac{3π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{4}$ |
分析 根据平面向量的数量积的定义解答.
解答 解:设$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为θ,
∵$\overrightarrow{b}$=(1,1),
∴|$\overrightarrow{b}$|=$\sqrt{2}$,
∵$\overrightarrow a•(\overrightarrow a-2\overrightarrow b)=3$,且$|\overrightarrow a|=1$,
∴|$\overrightarrow{a}$|2-2$\overrightarrow{a}•\overrightarrow{b}$=1-2|$\overrightarrow{a}$|•|$\overrightarrow{b}$|cosθ=3,
∴cosθ=-$\frac{\sqrt{2}}{2}$,
∵0≤θ≤π,
∴θ=$\frac{3π}{4}$,
故选:B
点评 本题考查了向量的数量积的定义以及向量模的运用求向量的夹角,属于基础题.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目
19.在△ABC中,如果a:b:c=2:$\sqrt{6}$:($\sqrt{3}$+1),则△ABC最小角为( )
| A. | $\frac{π}{4}$ | B. | $\frac{π}{6}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{12}$ |
2.下列说法中,正确的是( )
| A. | 小于$\frac{π}{2}$的角是锐角 | |
| B. | 第一象限的角不可能是负角 | |
| C. | 终边相同的两个角的差是360°的整数倍 | |
| D. | 若α是第一象限角,则2α是第二象限角 |
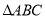 中,
中,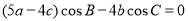 .
.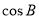 的值;
的值;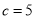 ,b=
,b=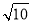 ,求
,求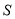 .
. 在某校趣味运动会的颁奖仪式上,为了活跃气氛,大会组委会决定在颁奖过程中进行抽奖活动,用分层抽样的方法从参加颁奖仪式的高一、高二、高三代表队中抽取20人前排就座,其中高二代表队有5人.
在某校趣味运动会的颁奖仪式上,为了活跃气氛,大会组委会决定在颁奖过程中进行抽奖活动,用分层抽样的方法从参加颁奖仪式的高一、高二、高三代表队中抽取20人前排就座,其中高二代表队有5人.