题目内容
已知在数列{an}中,a1=3,点(an,an+1)在直线y=x+2上,若数列{bn}满足bn=an•3n,记Tn是数列{bn}的前n项的和,那么Tn= .
考点:数列的求和
专题:等差数列与等比数列
分析:由已知得an+1=an+2,从而数列{an}是以3为首项,以2为公差的等差数列,an=3+2(n-1)=2n+l,从而bn=(2n+1)•3n,由此能求出{bn}的前n项的和.
解答:
解:∵点(an,an+1)在直线y=x+2上,
∴an+1=an+2,即an+1-an=2,
∴数列{an}是以3为首项,以2为公差的等差数列,
∴an=3+2(n-1)=2n+l.
∵bn=an•3n,
∴bn=(2n+1)•3n,
∴Tn=3×3+5×32+7×33+…+(2n+1)•3n,①
∴3Tn=3×32+5×33+…+(2n-1)•3n+(2n+1)•3n+1,②
①-②,得-2Tn=3×3+2(32+33+…+3n)-(2n+1)•3n+1
=9+2×
-(2n+1)•3n+1
=-2n•3n+1,
∴Tn=n•3n+1.
故答案为:n•3n+1.
∴an+1=an+2,即an+1-an=2,
∴数列{an}是以3为首项,以2为公差的等差数列,
∴an=3+2(n-1)=2n+l.
∵bn=an•3n,
∴bn=(2n+1)•3n,
∴Tn=3×3+5×32+7×33+…+(2n+1)•3n,①
∴3Tn=3×32+5×33+…+(2n-1)•3n+(2n+1)•3n+1,②
①-②,得-2Tn=3×3+2(32+33+…+3n)-(2n+1)•3n+1
=9+2×
| 9(1-3n-1) |
| 1-3 |
=-2n•3n+1,
∴Tn=n•3n+1.
故答案为:n•3n+1.
点评:本题考查数列的前n项和的求法,是中档题,解题时要认真审题,注意错位相减法的合理运用.

练习册系列答案
相关题目
设全集为R,函数f(x)=
的定义域为M,函数f(x)=ln(x2-4x)的定义域为N,则M∩N=( )
| 4-x2 |
| A、[-2,0) |
| B、(-∞,-2] |
| C、(4,+∞) |
| D、(-∞,0]∪(4,+∞) |
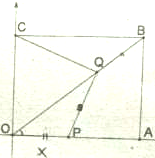 如图,在矩形OABC中,O为原点,B点坐标为(8,6).
如图,在矩形OABC中,O为原点,B点坐标为(8,6).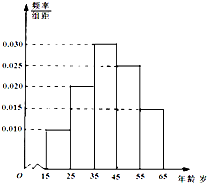 为了了解我市各景点在大众中的熟知度,随机对15~65岁的人群抽样了n人,回答问题“我市有哪几个著名的旅游景点?”,统计结果见下表和各组人数的频率分布直方图(如图):
为了了解我市各景点在大众中的熟知度,随机对15~65岁的人群抽样了n人,回答问题“我市有哪几个著名的旅游景点?”,统计结果见下表和各组人数的频率分布直方图(如图):