题目内容
已知对任意平面向量
=(x,y),把
绕其起点沿逆时针方向旋转θ角得到向量:
=(xcosθ-ysinθ,xsinθ+ycosθ),叫做把点B绕点A逆时针方向旋转θ角得到点P.
(1)已知平面内点A(1,2),点B(-1,2-2
),把点B绕点A逆时针方向旋转
后得到点P的坐标是 .
(2)设平面内曲线C:y=-
上的每一点绕坐标原点沿逆时针方向旋转
后得到的点的轨迹方程是: .
| AB |
| AB |
| AP |
(1)已知平面内点A(1,2),点B(-1,2-2
| 3 |
| π |
| 3 |
(2)设平面内曲线C:y=-
| 1 |
| 2x |
| π |
| 4 |
考点:轨迹方程,向量在几何中的应用
专题:平面向量及应用
分析:(1)由已知求出
的坐标,设出P的坐标,结合题目中定义即可列示求得P点坐标;
(2)分别设出旋转后得到的轨迹上的点的坐标及原曲线上点的坐标,结合题目中定义得到两坐标的关系,代入原曲线方程整理即可得到旋转后的点的轨迹方程.
| AB |
(2)分别设出旋转后得到的轨迹上的点的坐标及原曲线上点的坐标,结合题目中定义得到两坐标的关系,代入原曲线方程整理即可得到旋转后的点的轨迹方程.
解答:
解:(1)∵A(1,2),B(-1,2-2
),
∴
=(-2,-2
),
设P(x,y),则
=(x-1,y-2),
由题目中定义得:
.
解得:
.
∴点P的坐标是(-3,2);
(2)设旋转后得到的轨迹上的点为(x,y),
原曲线C:y=-
上的点为(x′,y′),
则
,
解得:
.
代入y=-
,得x′y′=-
,
即x2-y2=1.
故答案为:(1)(-3,2);(2)x2-y2=1.
| 3 |
∴
| AB |
| 3 |
设P(x,y),则
| AP |
由题目中定义得:
|
解得:
|
∴点P的坐标是(-3,2);
(2)设旋转后得到的轨迹上的点为(x,y),
原曲线C:y=-
| 1 |
| 2x |
则
|
解得:
|
代入y=-
| 1 |
| 2x |
| 1 |
| 2 |
即x2-y2=1.
故答案为:(1)(-3,2);(2)x2-y2=1.
点评:本题是新定义题,考查了轨迹方程的求法,训练了向量在几何中的应用,关键是对题意的理解,是中档题.

练习册系列答案
相关题目
函数f(x)=xln|x|(x≠0)的大致图象是( )
A、 |
B、 |
C、 |
D、 |
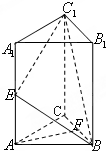 如图,在正三棱柱ABC-A1B1C1中,AB=2,AA1=4,E、F分别为AA1、BC的中点.
如图,在正三棱柱ABC-A1B1C1中,AB=2,AA1=4,E、F分别为AA1、BC的中点.