题目内容
14.各项均不为零的数列{an}的前n项和为Sn. 对任意n∈N*,$\overrightarrow{m_n}=({a_{n+1}}-{a_n},\;2{a_{n+1}})$都是直线y=kx的法向量.若$\lim_{n→∞}{S_n}$存在,则实数k的取值范围是(-∞,-1)∪(0,+∞).分析 由题意,数列的公比q满足0<|q|<1,对任意n∈N*,$\overrightarrow{m_n}=({a_{n+1}}-{a_n},\;2{a_{n+1}})$都是直线y=kx的法向量,则k=-$\frac{{a}_{n+1}-{a}_{n}}{2{a}_{n+1}}$=-$\frac{1}{2}$+$\frac{1}{2}$•$\frac{1}{q}$,由此,即可求出实数k的取值范围.
解答 解:由题意,数列的公比q满足0<|q|<1,
∵对任意n∈N*,$\overrightarrow{m_n}=({a_{n+1}}-{a_n},\;2{a_{n+1}})$都是直线y=kx的法向量,
∴k=-$\frac{{a}_{n+1}-{a}_{n}}{2{a}_{n+1}}$=-$\frac{1}{2}$+$\frac{1}{2}$•$\frac{1}{q}$,
∴k∈(-∞,-1)∪(0,+∞),
故答案为(-∞,-1)∪(0,+∞).
点评 本题考查数列的极限,考查向量知识的运用,属于中档题.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
4.已知$\overrightarrow a=({sin\frac{ω}{2}x,sinωx}),\overrightarrow b=({sin\frac{ω}{2}x,\frac{1}{2}})$,其中ω>0,若函数$f(x)=\overrightarrow a•\overrightarrow b-\frac{1}{2}$在区间(π,2π)内没有零点,则ω的取值范围是( )
| A. | $({0,\frac{1}{8}}]$ | B. | $({0,\frac{5}{8}}]$ | C. | $({0,\frac{1}{8}}]∪[{\frac{5}{8},1}]$ | D. | $({0,\frac{1}{8}}]∪[{\frac{1}{4},\frac{5}{8}}]$ |
 如图ABC-A1B1C1是直三棱柱,底面△ABC是等腰直角三角形,且AB=AC=4,直三棱柱的高等于4,线段B1C1的中点为D,线段BC的中点为E,线段CC1的中点为F.
如图ABC-A1B1C1是直三棱柱,底面△ABC是等腰直角三角形,且AB=AC=4,直三棱柱的高等于4,线段B1C1的中点为D,线段BC的中点为E,线段CC1的中点为F.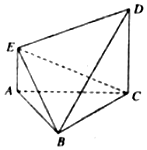 如图,△ABC为边长为2的正三角形,AE∥CD,且AE⊥平面ABC,2AE=CD=2.
如图,△ABC为边长为2的正三角形,AE∥CD,且AE⊥平面ABC,2AE=CD=2.