题目内容
2.设f-1(x)为$f(x)=\frac{2x}{x+1}$的反函数,则f-1(1)=1.分析 根据反函数的性质,原函数的值域是反函数的定义域即可求解
解答 解:$f(x)=\frac{2x}{x+1}$的反函数,
其反函数f-1(x),
反函数的性质,反函数的定义域是原函数的值域,即$\frac{2x}{x+x}=1$.
可得:x=1,
∴f-1(x)=1.
故答案为1.
点评 本题考查了反函数的性质,原函数与反函数的定义域和值域关系.比较基础.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
12.设函数f(x)=logax(a>0,a≠1)的图象过点($\frac{1}{8}$,3),则a的值为( )
| A. | 2 | B. | -2 | C. | $-\frac{1}{2}$ | D. | $\frac{1}{2}$ |
17.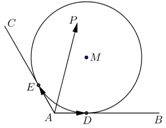 如图所示,∠BAC=$\frac{2π}{3}$,圆M与AB,AC分别相切于点D,E,AD=1,点P是圆M及其内部任意一点,且$\overrightarrow{AP}=x\overrightarrow{AD}+y\overrightarrow{AE}$(x,y∈R),则x+y的取值范围是( )
如图所示,∠BAC=$\frac{2π}{3}$,圆M与AB,AC分别相切于点D,E,AD=1,点P是圆M及其内部任意一点,且$\overrightarrow{AP}=x\overrightarrow{AD}+y\overrightarrow{AE}$(x,y∈R),则x+y的取值范围是( )
 如图所示,∠BAC=$\frac{2π}{3}$,圆M与AB,AC分别相切于点D,E,AD=1,点P是圆M及其内部任意一点,且$\overrightarrow{AP}=x\overrightarrow{AD}+y\overrightarrow{AE}$(x,y∈R),则x+y的取值范围是( )
如图所示,∠BAC=$\frac{2π}{3}$,圆M与AB,AC分别相切于点D,E,AD=1,点P是圆M及其内部任意一点,且$\overrightarrow{AP}=x\overrightarrow{AD}+y\overrightarrow{AE}$(x,y∈R),则x+y的取值范围是( )| A. | $[1,4+2\sqrt{3}]$ | B. | $[4-2\sqrt{3},4+2\sqrt{3}]$ | C. | $[1,2+\sqrt{3}]$ | D. | $[2-\sqrt{3},2+\sqrt{3}]$ |
12.某一算法框图如图所示,则输出的S值为( )
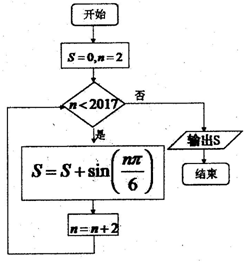

| A. | $\frac{{\sqrt{3}}}{2}$ | B. | $-\frac{{\sqrt{3}}}{2}$ | C. | $\sqrt{3}$ | D. | 0 |