题目内容
在△ABC中,三边a,b,c成等差数列,B=60°,S△ABC=
+
,则b的值是( )
| 3 |
| 2 |
| 3 |
A、
| ||||
B、
| ||||
C、3+
| ||||
D、
|
考点:正弦定理
专题:解三角形
分析:利用三边成等差数列得出b和a,c的关系,进而利用余弦定理求得a=c,推断出三角形为正三角形,进而利用三角形面积公式求得b.
解答:
解:∵a,b,c成等差数列,
∴2b=a+c,
∴cosB=
=
=
,
整理求得a=c,
∵B=60°,
∴三角形为等边三角形,
∴S△ABC=
acsinB=
b2•
=
+
,
∴b2=2
+4=3+2
+1=(
+1)2,
∴b=
+1.
故选B.
∴2b=a+c,
∴cosB=
| a2+c2-b2 |
| 2ac |
a2+c2-
| ||
| 2ac |
| 1 |
| 2 |
整理求得a=c,
∵B=60°,
∴三角形为等边三角形,
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 3 |
| 2 |
| 3 |
∴b2=2
| 3 |
| 3 |
| 3 |
∴b=
| 3 |
故选B.
点评:本题主要考查了正弦定理和余弦定理的应用.解题的关键是求得a和c的关系.

练习册系列答案
相关题目
若x>0,y>0,则
的最小值为( )
| ||||
|
A、
| ||||
| B、1 | ||||
C、
| ||||
D、
|
函数y=sinx在点x=
处的导数是( )
| π |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
| D、1 |
设函数f(x)在[0,1]上的图象是连续不断的曲线,在开区间(0,1)内的导函数f′(x)恒不等于1,对任意x∈[0,1]都有0<f(x)<1,则方程f(x)=x在开区间(0,1)内实根的个数为( )
| A、4 | B、3 | C、2 | D、1 |
在(-π,4π)内与-
终边相同的角有( )个.
| 5π |
| 4 |
| A、0 | B、1 | C、2 | D、3 |
设随机变量的分布列如下表所示,且a+2b=1.3,则a-b=( )
| X | 0 | 1 | 2 | 3 |
| P | 0.1 | a | b | 0.1 |
| A、0.5 | B、0.3 |
| C、0.2 | D、-0.2 |
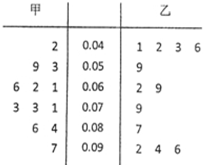 PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物,如图是根据某地某日早7点至晚8点甲、乙两个PM2.5监测点统计的数据(单位:毫克/每立方米)列出的茎叶图,则甲、乙两地浓度的方差较小的是
PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物,如图是根据某地某日早7点至晚8点甲、乙两个PM2.5监测点统计的数据(单位:毫克/每立方米)列出的茎叶图,则甲、乙两地浓度的方差较小的是