题目内容
已知定义在(-∞,0)∪(0,+∞)上的函数f(x)满足f(-x)=f(x),当a,b∈(-∞,0)时总有
>0(a≠b),若f(m+1)>f(2m),则实数m的取值范围是 .
| f(a)-f(b) |
| a-b |
考点:函数奇偶性的性质
专题:函数的性质及应用
分析:本题可先通过函数是偶函数将原不等式中的函数自变量转化为非负数,再利用函数的单调性研究,将不等式转化为两个自变量的大小比较,解不等式,得到本题结论.
解答:
解:∵定义在(-∞,0)∪(0,+∞)上的函数f(x)满足f(-x)=f(x),
∴f(x)是偶函数,且f(-x)=f(x)=f(|x|).
∵当a,b∈(-∞,0)时总有
>0(a≠b),
∴f(x)在(-∞,0)上单调递增,
∴f(x)在(0,+∞)上单调递减.
∵f(m+1)>f(2m),
∴f(|m+1|)>f(|2m|),
∴0<|m+1|<|2m|,
∴4m2>(m+1)2>0,
∴
,
∴m<-1或-1<m<-
或m>1.
∴实数m的取值范围是(-∞,-1)∪(-1,-
)∪(1,+∞).
故答案为:(-∞,-1)∪(-1,-
)∪(1,+∞).
∴f(x)是偶函数,且f(-x)=f(x)=f(|x|).
∵当a,b∈(-∞,0)时总有
| f(a)-f(b) |
| a-b |
∴f(x)在(-∞,0)上单调递增,
∴f(x)在(0,+∞)上单调递减.
∵f(m+1)>f(2m),
∴f(|m+1|)>f(|2m|),
∴0<|m+1|<|2m|,
∴4m2>(m+1)2>0,
∴
|
∴m<-1或-1<m<-
| 1 |
| 3 |
∴实数m的取值范围是(-∞,-1)∪(-1,-
| 1 |
| 3 |
故答案为:(-∞,-1)∪(-1,-
| 1 |
| 3 |
点评:本题考查了函数的奇偶性、函数的单调性、函数的定义域、不等式的解法,还考查了化归转化的数学思想和分析问题解决问题的能力,本题有一定的综合性,属于中档题.

练习册系列答案
相关题目
要得到函数y=cos(x+1)的图象,只要将函数y=cosx的图象( )
| A、向左平移1个单位 | ||
| B、向右平移1个单位 | ||
C、向左平移
| ||
D、向右平移
|
已知函数f(x)=(x-a)(x-b),(a>b)的图象如图所示,则g(x)=ax+b的图象经过( )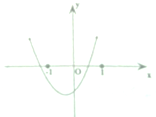

| A、第一、二、三象限 |
| B、第一、二、四象限 |
| C、第一、三、四象限 |
| D、第二、三、四象限 |