题目内容
 已知函数f(x)=Asin(ωx+φ)(x?R,A>0,ω>0,0<φ<
已知函数f(x)=Asin(ωx+φ)(x?R,A>0,ω>0,0<φ<| π |
| 2 |
| 5 |
| 13 |
(1)求函数y=f(x)的解析式;
(2)将函数y=f(x)的图象向右平移2个单位后得到函数y=g(x)的图象,当x∈(-1,2)时,求函数h(x)=f(x)•g(x)的值域.
考点:由y=Asin(ωx+φ)的部分图象确定其解析式,正弦函数的图象,函数y=Asin(ωx+φ)的图象变换
专题:三角函数的图像与性质
分析:(1)从给出的三角函数图象中给出三个线段信息,从中可以求出图象最高点的坐标,
的长度,由此推理出三角函数的解析式;
(2)由题意先求出g(x),h(x)的函数解析式,由x的范围求出
x-
的范围,同时结合三角函数的图象进行分析,即可求出其函数值域.
| T |
| 4 |
(2)由题意先求出g(x),h(x)的函数解析式,由x的范围求出
| π |
| 3 |
| π |
| 6 |
解答:
解:(1)由条件知cos∠POQ=
=
,所以P(1,2). (2分)
由此可得振幅A=2,周期T=4×(4-1)=12,又
=12,则ω=
.
将点P(1,2)代入f(x)=2sin(
x+φ),得sin(
x+φ)=1,
因为0<φ<
,所以φ=
,于是f(x)=2sin(
x+
). (6分)
(2)由题意可得g(x)=2sin[
(x-2)+
]=2sin
x.
所以h(x)=f(x)•g(x)=4sin(
x+
)•sin
x=2sin2
x+2
sin
x•cos
x=1-cos
x+
sin
x=1+2sin(
x-
). (9分)
当x∈(-1,2)时,
x-
∈(-
,
),所以sin(
x-
)∈(-1,1),
即1+2sin(
x-
)∈(-1,3).于是函数h(x)的值域为(-1,3). (12分)
42+(
| ||||
2×4×
|
| ||
| 5 |
由此可得振幅A=2,周期T=4×(4-1)=12,又
| 2π |
| ω |
| π |
| 6 |
将点P(1,2)代入f(x)=2sin(
| π |
| 6 |
| π |
| 6 |
因为0<φ<
| π |
| 2 |
| π |
| 3 |
| π |
| 6 |
| π |
| 3 |
(2)由题意可得g(x)=2sin[
| π |
| 6 |
| π |
| 3 |
| π |
| 6 |
所以h(x)=f(x)•g(x)=4sin(
| π |
| 6 |
| π |
| 3 |
| π |
| 6 |
| π |
| 6 |
| 3 |
| π |
| 6 |
| π |
| 6 |
| π |
| 3 |
| 3 |
| π |
| 3 |
| π |
| 3 |
| π |
| 6 |
当x∈(-1,2)时,
| π |
| 3 |
| π |
| 6 |
| π |
| 2 |
| π |
| 2 |
| π |
| 3 |
| π |
| 6 |
即1+2sin(
| π |
| 3 |
| π |
| 6 |
点评:本题主要考查了三角函数图象的平移、三角函数的恒等变换及三角函数的值域等知识,考查了求解三角函数的值域,关注自变量x的取值范围是解题的关键,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知函数f(x)是定义在[-1,1]上的奇函数,对于任意x1,x2∈[-1,1],x1≠x2总有
>0且f(1)=1.若对于任意a∈[-1,1],存在x∈[-1,1],使f(x)≤t2-2at-1成立,则实数t的取值范围是( )
| f(x1)-f(x2) |
| x1-x2 |
| A、-2≤t≤2 | ||||
B、t≤-1-
| ||||
| C、t≤0或t≥2 | ||||
| D、t≥2或t≤-2或t=0 |
若向量
=(1,-2),
=(2,1),
=(-4,-2),则下列说法中错误的是( )
| a |
| b |
| c |
A、
| ||||||||
B、向量
| ||||||||
C、
| ||||||||
D、对同一平面内的任意向量
|
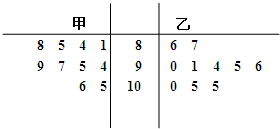 甲、乙两所学校高三级某学年10次联合考试的理科数学成绩平均分用茎叶图如图所示,则甲乙两所学校的平均分
甲、乙两所学校高三级某学年10次联合考试的理科数学成绩平均分用茎叶图如图所示,则甲乙两所学校的平均分. |
| x |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|