题目内容
若向量
=(1,-2),
=(2,1),
=(-4,-2),则下列说法中错误的是( )
| a |
| b |
| c |
A、
| ||||||||
B、向量
| ||||||||
C、
| ||||||||
D、对同一平面内的任意向量
|
考点:数量积表示两个向量的夹角,平行向量与共线向量,平面向量的基本定理及其意义,平面向量数量积的运算
专题:平面向量及应用
分析:由向量的平行垂直关系和平面向量基本定理,逐个选项验证即可.
解答:
解:∵向量
=(1,-2),
=(2,1),
=(-4,-2),
∴
•
=1×2-2×1=0,∴
⊥
,A正确;
同理可得
•
=1×(-4)-2×(-2)=0,∴
⊥
,B正确;
∵
=-2
,∴
∥
,C正确;
∵
∥
,∴
和
不能作基底,D错误.
故选:D
| a |
| b |
| c |
∴
| a |
| b |
| a |
| b |
同理可得
| a |
| c |
| a |
| c |
∵
| c |
| b |
| b |
| c |
∵
| b |
| c |
| b |
| c |
故选:D
点评:本题考查平面向量的共线和垂直,以及平面向量基本定理,属基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知条件p:x2-3x-4≤0,条件q:x2-6x+9-m2≤0.若p是q的充分不必要条件,则m的取值范围是( )
| A、[-1,1] |
| B、[-4,4] |
| C、(-∞,-4]∪[4,+∞) |
| D、(-∞,-1]∪[4,+∞) |
某几何体三视图如图所示,则该几何体的体积为( )
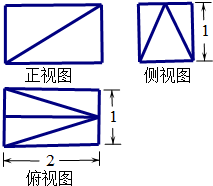

A、
| ||
| B、1 | ||
C、
| ||
D、
|
设a=log3
,b=log5
,c=log7
,则( )
| 2 |
| 3 |
| 2 |
| 5 |
| 2 |
| 7 |
| A、c>b>a |
| B、b>c>a |
| C、a>c>b |
| D、a>b>c |
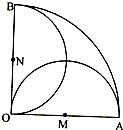 如图,在圆心角为直角的扇形OAB区域中,M、N分别为OA、OB的中点,在M、N两点处各有一个通信基站,其信号的覆盖范围分别为以OA、OB为直径的圆,在扇形OAB内随机取一点,则此点无信号的概率是( )
如图,在圆心角为直角的扇形OAB区域中,M、N分别为OA、OB的中点,在M、N两点处各有一个通信基站,其信号的覆盖范围分别为以OA、OB为直径的圆,在扇形OAB内随机取一点,则此点无信号的概率是( )A、1-
| ||||
B、
| ||||
C、
| ||||
D、
|
 已知函数f(x)=Asin(ωx+φ)(x?R,A>0,ω>0,0<φ<
已知函数f(x)=Asin(ωx+φ)(x?R,A>0,ω>0,0<φ<