题目内容
19．设f（x）是R上的偶函数，且在[0，+∞）上是单调递增，若f（2）=0，则使f（log${\;}_{\frac{1}{2}}$x）＜0成立的x的取值范围是（ ）| A． | （$\frac{\sqrt{2}}{2}$，4） | B． | （0，$\frac{1}{4}$） | C． | （$\frac{1}{4}$，$\frac{\sqrt{2}}{2}$） | D． | （$\frac{1}{4}$，4） |
分析 根据函数奇偶性和单调性之间的关系，将不等式进行转化即可得到结论．
解答 解：∵f（x）是R上的偶函数，且在[0，+∞）上是增函数，又f（2）=0，
∴不等式f（log${\;}_{\frac{1}{2}}$x）＜0等价为f（|log${\;}_{\frac{1}{2}}$x|）＜f（2），
即|log${\;}_{\frac{1}{2}}$x|＜2，
则-2＜log${\;}_{\frac{1}{2}}$x＜2，
解得$\frac{1}{4}$＜x＜4，
故选：D．
点评 本题主要考查不等式的解法，根据函数奇偶性和单调性之间的关系将不等式进行转化是解决本题的关键．
练习册系列答案
相关题目
10．下列函数在其定义域上既是奇函数又是减函数的是（ ）
| A． | f（x）=2x | B． | f（x）=log${\;}_{\frac{1}{2}}$x | C． | f（x）=$\frac{1}{x}$ | D． | f（x）=-x|x| |
7．函数y=3-2cos（2x-$\frac{π}{3}$）的单调递减区间是（ ）
| A． | （kπ+$\frac{π}{6}$，kπ+$\frac{2π}{3}$）（k∈Z） | B． | （kπ-$\frac{π}{3}$，kπ+$\frac{π}{6}$）（k∈Z） | ||
| C． | （2kπ+$\frac{π}{3}$，2kπ+$\frac{4π}{3}$）（k∈Z） | D． | （2kπ-$\frac{π}{3}$，2kπ+$\frac{π}{6}$）（k∈Z） |
14．下列各组中的函数f（x），g（x）表示同一函数的是（ ）
| A． | f（x）=x，g（x）=${（\sqrt{x}\;）^2}$ | B． | f（x）=x+1，g（x）=$\frac{{{x^2}-1}}{x-1}$ | ||
| C． | f（x）=|x|，g（x）=$\sqrt{{x}^{2}}$ | D． | f（x）=log22x，g（x）=2log2x |
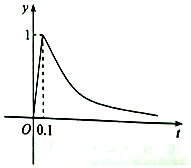雾霾是人体健康的隐形杀手，爱护环境，人人有责．某环保实验室在雾霾天采用清洁剂处理教室空气质量．实验发现，当在教室释放清洁剂的过程中，空气中清洁剂的含剂浓度y（mg/m3）与时间t（h）成正比；释放完毕后，y与t的函数关系为y=（$\frac{1}{16}$）t-a（a为常数），如图，已知当教室的空气中含剂浓度在0.25mg/m3以上时，教室最适合人体活动．根据图中信息，从一次释放清洁剂开始，这间教室有0.575h最适合人体活动．
11．阅读下边的程序框图，运行相应的程序，则输出v的值为（ ）
| A． | 4 | B． | 5 | C． | 6 | D． | 7 |
8．已知集合A={0，1，4}，B={y|y=x2，x∈A}，则A∪B=（ ）
| A． | {0，1，16} | B． | {0，1} | C． | {1，16} | D． | {0，1，4，16} |