题目内容
10．若x，y满足约束条件$\left\{\begin{array}{l}x-2≥0\\ x-y≤0\\ x+y-6≤0\end{array}\right.$，那么$\frac{y}{x}$的最大值是2．分析 作出不等式组对应的平面区域，利用z的几何意义结合直线的斜率公式进行求解即可．
解答 
解：作出不等式组对应的平面区域，
那么z=$\frac{y}{x}$的几何意义是区域内的点到定点（0，0）的斜率
由图象知OB的斜率最大，
由$\left\{\begin{array}{l}{x=2}\\{x+y=6}\end{array}\right.$可得B（2，4），
∴z的最大值为z=$\frac{4}{2}$=2，
故答案为：2．
点评 本题主要考查线性规划的应用，利用直线斜率的几何意义以及数形结合是解决本题的关键．
练习册系列答案
赢在课堂名师课时计划系列答案
天天向上课时同步训练系列答案
阳光课堂同步练习系列答案
相关题目
1．如图是棱长为1的正方体的平面展开图，则在这个正方体中，以下结论错误的是（ ）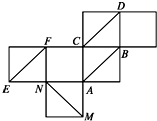
| A． | 点M到AB的距离为$\frac{{\sqrt{2}}}{2}$ | B． | AB与EF所成角是90° | ||
| C． | 三棱锥C-DNE的体积是$\frac{1}{6}$ | D． | EF与MC是异面直线 |
18．
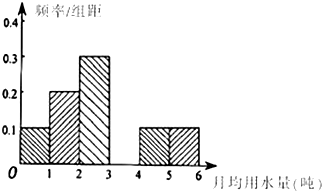为了解某市居民日常用水量的标准，某机构通过抽样获得了100位居民某年的月均用水量（单位：吨），如表是这100位居民月均用水量的频率分布表，根据如表解答下列问题：
（1）求如表中a和b的值；
（2）请将下面的频率分布直方图补充完整，并根据直方图估计该市每位居民月均用水量的中位数（精确到0.01）．
为了解某市居民日常用水量的标准，某机构通过抽样获得了100位居民某年的月均用水量（单位：吨），如表是这100位居民月均用水量的频率分布表，根据如表解答下列问题：（1）求如表中a和b的值；
（2）请将下面的频率分布直方图补充完整，并根据直方图估计该市每位居民月均用水量的中位数（精确到0.01）．
| 分组 | 频数 | 频率 |
| [0，1） | 10 | b |
| [1，2） | 20 | 0.20 |
| [2，3） | a | 0.30 |
| [3，4） | 20 | 0.20 |
| [4，5） | 10 | 0.10 |
| [5，6] | 10 | 0.10 |
| 合计 | 100 | 1.00 |
5．一台机器由于使用时间较长，但还可以使用，它按不同的转速生产出来的某机器零件有一些会有缺点，每小时生产有缺点零件的多少随机器运转的速度而变化，如表是抽样试验结果：
若实际生产中，允许每小时的产品中有缺点的零件数最多为10个，那么机器的转速应该控制所在的范围是（ ）
| 转速x/（rad/s） | 16 | 14 | 12 | 8 |
| 每小时生产有缺点的零件数y/件 | 11 | 9 | 8 | 5 |
| A． | 10转/s以下 | B． | 15转/s以下 | C． | 20转/s以下 | D． | 25转/s以下 |
2．已知命题p：“x∈R时，都有x2-x+$\frac{1}{4}$＜0”；命题q：“存在x∈R，使sinx+cosx=$\sqrt{2}$成立”．则下列判断正确的是（ ）
| A． | p∨q为假命题 | B． | p∧q为真命题 | C． | ￢p∧q为真命题 | D． | ￢p∨￢q是假命题 |
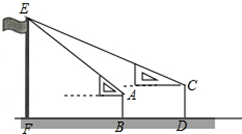某校高一年级某班开展数学活动，小李和小军合作用一副三角板测量学校的旗杆，小李站在B点测得旗杆顶端E点的仰角为45°，小军站在点D测得旗杆顶端E点的仰角为30°，已知小李和小军相距（BD）6米，小李的身高（AB）1.5米，小军的身高（CD）1.75米，求旗杆的高EF的长．（结果精确到0.1，参考数据：$\sqrt{2}$≈1.41，$\sqrt{3}$≈1.73）
20．已知全集U={1，2，3，4，5，6，7，8}，集合A={2，3，5，6}，集合B={1，3，4，6，7}，则集合A∩（∁UB）等于（ ）
| A． | {2，5} | B． | {3，6} | C． | {2，5，6} | D． | {2，3，5，6，8} |