题目内容
已知函数f(x)=
(1)若a∈(-2,2),求f(x)的单调区间;
(2)求f(x)值域;
(3)若a>-2,求f(x)在区间[0,1]上的最大值和最小值.
| 1 |
| x2+ax+1 |
(1)若a∈(-2,2),求f(x)的单调区间;
(2)求f(x)值域;
(3)若a>-2,求f(x)在区间[0,1]上的最大值和最小值.
考点:利用导数研究函数的单调性,利用导数求闭区间上函数的最值
专题:导数的综合应用
分析:(1)由a∈(-2,2)得△=a2-4<0,对任意x∈R,f(x)>0,令u=x2+ax+1,易知u在(-∞,-
)上递减,在(-
,+∞)上递增,于是f(x)的递增区间是(-∞,-
),递减区间是(-
,+∞).
(2)讨论(ⅰ)当a∈(-2,2)时(ⅱ)当a=±2时(ⅲ)当a∈(-∞,-2)∪(2,+∞)时综合得出结论.
(3)讨论(ⅰ)当a∈[0,+∞)时,(ⅱ)当a∈[-1,0)时(ⅲ)当a∈(-2,-1)时从而综合得出结论.
| a |
| 2 |
| a |
| 2 |
| a |
| 2 |
| a |
| 2 |
(2)讨论(ⅰ)当a∈(-2,2)时(ⅱ)当a=±2时(ⅲ)当a∈(-∞,-2)∪(2,+∞)时综合得出结论.
(3)讨论(ⅰ)当a∈[0,+∞)时,(ⅱ)当a∈[-1,0)时(ⅲ)当a∈(-2,-1)时从而综合得出结论.
解答:
解:(1)∵a∈(-2,2),
∴△=a2-4<0,对任意x∈R,f(x)>0,令u=x2+ax+1,
易知u在(-∞,-
)上递减,在(-
,+∞)上递增,
于是f(x)的递增区间是(-∞,-
),递减区间是(-
,+∞).
(2)(ⅰ)当a∈(-2,2)时,umin=u(-
)=
,
结合(1)得f(x)的值域是(0,
),
(ⅱ)当a=±2时,f(x)=
或f(x)=
,f(x)值域均为(0,+∞),
(ⅲ)当a∈(-∞,-2)∪(2,+∞)时,△=a2-4>0,方程x2+ax+1=0有两实根x1,x2(不妨设x1<x2),
与(1)同理,f(x)在(-∞,x1)上递增,在(x1,-
)上递增,在(-
,x2)上递减,在(x2,+∞)上递减,
且x∈(-∞,x1)∪(x2,+∞)时,f(x)>0,
当x→x1(x<x1)时f(x)→+∞,所以f(x)∈(0,+∞),
同理,当x∈(x1,x2)时,f(x)∈(-∞,
),
综上,当a∈(-∞,-2)∪(2,+∞)时,f(x)值域为(-∞,
)∪(0,+∞).
(3)(ⅰ)当a∈[0,+∞)时,
∵-
<0,且u(0)=1>0,于是x2+ax+1≥1,且f(x)在[0,1]上递减,
因此,fmax(x)=1,fmin(x)=
,
(ⅱ)当a∈[-1,0)时,-
∈(0,
],
此时,f(x)在[0,-
)上递增,在[-
,1]上递减,
且f(0)=1≥
=f(1),
所以fmax(x)=
,fmin(x)=
,
(ⅲ)当a∈(-2,-1)时,单调性同上,不过此时f(0)=1<
=f(1),
所以fmax(x)=
,fmin(x)=1.
综上所述,
当a∈[0,+∞)时,fmax(x)=1,fmin(x)=
,
当a∈[-1,0)时,-
∈(0,
],fmax(x)=
,fmin(x)=
,
当a∈(-2,-1)时,fmax(x)=
,fmin(x)=1.
∴△=a2-4<0,对任意x∈R,f(x)>0,令u=x2+ax+1,
易知u在(-∞,-
| a |
| 2 |
| a |
| 2 |
于是f(x)的递增区间是(-∞,-
| a |
| 2 |
| a |
| 2 |
(2)(ⅰ)当a∈(-2,2)时,umin=u(-
| a |
| 2 |
| 4-a2 |
| 4 |
结合(1)得f(x)的值域是(0,
| 4 |
| 4-a2 |
(ⅱ)当a=±2时,f(x)=
| 1 |
| (x-1)2 |
| 1 |
| (x+1)2 |
(ⅲ)当a∈(-∞,-2)∪(2,+∞)时,△=a2-4>0,方程x2+ax+1=0有两实根x1,x2(不妨设x1<x2),
与(1)同理,f(x)在(-∞,x1)上递增,在(x1,-
| a |
| 2 |
| a |
| 2 |
且x∈(-∞,x1)∪(x2,+∞)时,f(x)>0,
当x→x1(x<x1)时f(x)→+∞,所以f(x)∈(0,+∞),
同理,当x∈(x1,x2)时,f(x)∈(-∞,
| 4 |
| 4-a2 |
综上,当a∈(-∞,-2)∪(2,+∞)时,f(x)值域为(-∞,
| 4 |
| 4-a2 |
(3)(ⅰ)当a∈[0,+∞)时,
∵-
| a |
| 2 |
因此,fmax(x)=1,fmin(x)=
| 1 |
| a+2 |
(ⅱ)当a∈[-1,0)时,-
| a |
| 2 |
| 1 |
| 2 |
此时,f(x)在[0,-
| a |
| 2 |
| a |
| 2 |
且f(0)=1≥
| 1 |
| a+2 |
所以fmax(x)=
| 4 |
| 4-a2 |
| 1 |
| a+2 |
(ⅲ)当a∈(-2,-1)时,单调性同上,不过此时f(0)=1<
| 1 |
| a+2 |
所以fmax(x)=
| 4 |
| 4-a2 |
综上所述,
当a∈[0,+∞)时,fmax(x)=1,fmin(x)=
| 1 |
| a+2 |
当a∈[-1,0)时,-
| a |
| 2 |
| 1 |
| 2 |
| 4 |
| 4-a2 |
| 1 |
| a+2 |
当a∈(-2,-1)时,fmax(x)=
| 4 |
| 4-a2 |
点评:本题考察了函数的单调性,导数的应用,渗透了分类讨论思想,是一道综合题.

练习册系列答案
相关题目
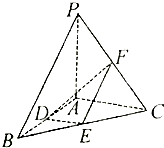 如图,在三棱锥P-ABC中,PA⊥平面ABC,∠BAC=90°,D、E、F分别是棱AB、BC、CP的中点,AB=AC=1,PA=2.
如图,在三棱锥P-ABC中,PA⊥平面ABC,∠BAC=90°,D、E、F分别是棱AB、BC、CP的中点,AB=AC=1,PA=2. 我国政府对PM2.5采用如下标准:
我国政府对PM2.5采用如下标准: