题目内容
19.某商店将进货价每个10元的商品按每个18元售出时,每天可卖出60个.商店经理到市场上做了一番调查后发现,若将这种商品的售价(在每个18元的基础上)每提高1元,则日销售量就减少5个;若将这种商品的售价(在每个18元的基础上)每降低1元,则日销售量就增加10个.为了每日获得最大利润,则此商品的售价应定为每个多少元?并求获得的最大利润.分析 设出该商品售价,求得销售量,可得利润函数,利用配方法,可得结论.
解答 解:设每个商品的售价定为x元时,每天所获得的利润为f(x),
10≤x≤18时,f(x)=(x-10)•[60+(18-x)×10]
=-10x 2+340x-2400,
=-10(x-17)2+490,
则x=17时最大利润f(x)=490.
①当x>18时,f(x)=(x-10)•[60-(x-18)×5]
=-5(x-20)2+500,
则x=20时最大利润f(x)=500,
综上可得当售价定为每个20元时,获得的最大利润为500元.
点评 此题主要考查了二次函数的应用,得到涨价后的销售量及把所给利润的关系式进行配方是解决本题的难点.

练习册系列答案
 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
10.设△ABC的内角A、B、C的对边分别为a、b、c,且A=60°,b=1,△ABC的面积S△ABC=$\frac{{\sqrt{3}}}{2}$,则$\frac{a+b+c}{sinA+sinB+sinC}$=( )
| A. | $\sqrt{3}$ | B. | $2\sqrt{3}$ | C. | 2 | D. | 4 |
7.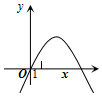 已知二次函数y=ax2+bx+c=0(a≠0)的图象如图所示,记p=|a-b+c|+|2a+b|,q=|a+b+c|+|2a-b|,则( )
已知二次函数y=ax2+bx+c=0(a≠0)的图象如图所示,记p=|a-b+c|+|2a+b|,q=|a+b+c|+|2a-b|,则( )
 已知二次函数y=ax2+bx+c=0(a≠0)的图象如图所示,记p=|a-b+c|+|2a+b|,q=|a+b+c|+|2a-b|,则( )
已知二次函数y=ax2+bx+c=0(a≠0)的图象如图所示,记p=|a-b+c|+|2a+b|,q=|a+b+c|+|2a-b|,则( )| A. | p>q | B. | p=q | ||
| C. | p<q | D. | p,q大小关系不能确定 |
14.下列表示正确的是( )
| A. | ∅∈{0} | B. | {3}∈{1,3} | C. | 0⊆{0,1} | D. | ∅⊆{2} |
11.已知过点P(-1,1)且斜率为k的直线l与抛物线y2=x有且只有一个交点,则k的值等于0或$\frac{{-1+\sqrt{2}}}{2}$或$\frac{{-1-\sqrt{2}}}{2}$.
9.已知cos($\frac{π}{2}$+α)=$\frac{3}{5}$,则α∈($\frac{π}{2}$,$\frac{3π}{2}$),则sin2α=( )
| A. | -$\frac{24}{25}$ | B. | -$\frac{16}{25}$ | C. | $\frac{24}{25}$ | D. | $\frac{12}{25}$ |