题目内容
已知复数z=（m-2）+（m2-9）i在复平面内对应的点位于第四象限，则实数m的取值范围是 ．
考点：复数的代数表示法及其几何意义
专题：数系的扩充和复数
分析：复数z=（m-2）+（m2-9）i在复平面内对应的点位于第四象限，可得
，解得即可．
|
解答：
解：∵复数z=（m-2）+（m2-9）i在复平面内对应的点位于第四象限，
∴
，解得2＜x＜3．
∴实数m的取值范围是（2，3）．
故答案为：（2，3）．
∴
|
∴实数m的取值范围是（2，3）．
故答案为：（2，3）．
点评：本题考查了复数的几何意义，属于基础题．
练习册系列答案
名师点拨卷系列答案
相关题目
已知一圆锥的侧面展开图是一个中心角为直角的扇形，若该圆锥的侧面积为4π，则该圆锥的体积为（ ）
A、
| ||||
B、
| ||||
| C、3π | ||||
D、
|
在△ABC中，根据下列条件解三角形，其中有两个解的是（ ）
| A、b=10，A=45°，C=70° |
| B、a=60，A=45°，B=60° |
| C、a=7，b=5，A=80° |
| D、b=14，b=16，C=45° |
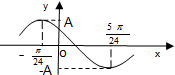已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，0＜φ＜π），其部分图象如图所示，且直线y=A与曲线y=f（x）（-
设集合M={x|x-m＜0}，N={y|y=ax-1，a＞0且a≠1}，若M∩N=∅，则m的范围是（ ）
| A、m≥-1 | B、m＞-1 |
| C、m≤-1 | D、m＜-1 |