题目内容
甲、乙等五名志愿者被随机地分到A、B、C、D四个不同的岗位服务,每个岗位至少有一名志愿者.设随机变量ξ为这五名志愿者中参加A岗位服务的人数,则ξ的数学期望为 .
考点:离散型随机变量的期望与方差
专题:概率与统计
分析:随机变量ξ可能取的值为1,2,事件“ξ=2”是指有两人同时参加A岗位服务,由此可得ξ的分布列,进而得到ξ的数学期望.
解答:
解:随机变量ξ可能取的值为1,2,事件“ξ=2”是指有两人同时参加A岗位服务,
则P(ξ=2)=
=
,
所以P(ξ=1)=1-P(ξ=2)=
,
即ξ的分布列如下表所示
…(10分)
∴ξ的数学期望E(ξ)=
×2+
×1=
,
故答案为:
则P(ξ=2)=
| ||||
|
| 1 |
| 4 |
所以P(ξ=1)=1-P(ξ=2)=
| 3 |
| 4 |
即ξ的分布列如下表所示
| ξ | 1 | 2 | ||||
| P |
|
|
∴ξ的数学期望E(ξ)=
| 1 |
| 4 |
| 3 |
| 4 |
| 5 |
| 4 |
故答案为:
| 5 |
| 4 |
点评:本题考查等可能事件的概率,考查离散型随机变量的概率与分布列和数学期望,属于中档题.

练习册系列答案
相关题目
若点(16,2)在函数y=logax(a>0且a≠1)的图象上,则tan
的值为( )
| aπ |
| 3 |
A、-
| ||||
B、-
| ||||
C、
| ||||
D、
|
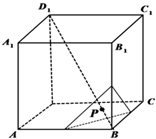 如图,正方体ABCD-A1B1C1D1的棱长为
如图,正方体ABCD-A1B1C1D1的棱长为| 3 |
| 1 |
| 2 |
| 5 |
| 2 |
A、[
| ||||||
B、[
| ||||||
C、[
| ||||||
D、[
|
等比数列{an}的前n项和为Sn,若a1=1,且4a1,2a2,a3成等差数列,则S6=( )
| A、63 | B、64 | C、31 | D、32 |