题目内容
14.已知函数f(x)=(log${\;}_{\frac{1}{4}}$x)2-log${\;}_{\frac{1}{4}}$x+5,x∈[1,4],求f(x)的最大值和最小值及对应的x值.分析 令t=log$\frac{1}{4}$x,则f(x)=y=t2-t+5,t∈[-1,0],结合二次函数的图象和性质,可得函数的最值
解答 解:令t=log$\frac{1}{4}$x,
∵x∈[1,4],
∴t∈[-1,0],
则f(t)=y=t2-t+5,
∵y=t2-t+5的图象是开口朝上,且以直线t=$\frac{1}{2}$为对称轴的抛物线,
故当t=-1时,函数最最大值7,当t=$\frac{1}{2}$时,函数取最小值为$\frac{19}{4}$.
点评 本题考查的知识点是二次函数的图象和性质,指数函数的图象和性质,函数的最值,难度中档.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
4.设数列{an}满足:a1=2,an+1=1-$\frac{1}{a_n}$,记数列{an}的前n项之积为Tn,则T2016的值为( )
| A. | -$\frac{1}{2}$ | B. | -1 | C. | $\frac{1}{2}$ | D. | 1 |
5.某几何体的三视图如图所示,当xy最大时,该几何体外接球的表面积为( )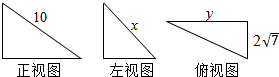

| A. | 32π | B. | 64π | C. | 128π | D. | 136π |
2.已知椭圆的两个焦点为F1(-$\sqrt{5}$,0),F2($\sqrt{5}$,0),M是椭圆上一点,若MF1⊥MF2,|MF1||MF2|=8,则该椭圆的方程是( )
| A. | $\frac{{x}^{2}}{7}$+$\frac{{y}^{2}}{2}$=1 | B. | $\frac{{x}^{2}}{2}$+$\frac{{y}^{2}}{7}$=1 | C. | $\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{4}$=1 | D. | $\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{9}$=1 |
3.已知函数f(x)=$\left\{\begin{array}{l}-{x^2}-2x(x≥0)\\{x^2}-2x(x<0)\end{array}$,又α,β为锐角三角形两锐角则( )
| A. | f(sinα)>f(cosβ) | B. | f(sinα)<f(cosβ) | C. | f(sinα)>f(sinβ) | D. | f(cosα)>f(cosβ) |
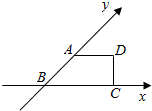 一个水平放置的平面图形的斜二测直观图是直角梯形ABCD,如图所示,∠ABC=45°,$AB=AD=\sqrt{2}$,DC⊥BC,这个平面图形的面积为$4+\sqrt{2}$.
一个水平放置的平面图形的斜二测直观图是直角梯形ABCD,如图所示,∠ABC=45°,$AB=AD=\sqrt{2}$,DC⊥BC,这个平面图形的面积为$4+\sqrt{2}$.