Question

9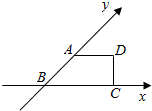．一个水平放置的平面图形的斜二测直观图是直角梯形ABCD，如图所示，∠ABC=45°，$AB=AD=\sqrt{2}$，DC⊥BC，这个平面图形的面积为$4+\sqrt{2}$．

Answer 1

分析 先确定直观图中的线段长，再确定平面图形中的线段长，即可求得图形的面积．

解答 解：在直观图中，∵∠ABC=45°，AB=AD=$\sqrt{2}$，DC⊥BC，
∴AD=$\sqrt{2}$，BC=1+$\sqrt{2}$，
∴原来的平面图形上底长为$\sqrt{2}$，下底为1+$\sqrt{2}$，高为2$\sqrt{2}$，
∴平面图形的面积为$\frac{1}{2}$（$\sqrt{2}$+1+$\sqrt{2}$）×2$\sqrt{2}$=$4+\sqrt{2}$，
故答案为：$4+\sqrt{2}$

点评 本题考查斜二测画法，直观图与平面图形的面积的比例关系的应用，考查计算能力