题目内容

5．某几何体的三视图如图所示，当xy最大时，该几何体外接球的表面积为（　　）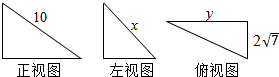
A．32πB．64πC．128πD．136π

分析 三视图复原几何体，x2+y2=128，利用基本不等式，确定xy最大时x=y=8，三棱锥扩充为长方体，对角线长为$\sqrt{100+28}$=$\sqrt{128}$=8$\sqrt{2}$，求出几何体外接球的半径，可得几何体外接球的表面积．

解答 解：由三视图得几何体为三棱锥，∴x2-28+y2=100，∴x2+y2=128，
∵2xy≤x2+y2，∴xy≤64，当x=y=8时，取“=”，
三棱锥扩充为长方体，对角线长为$\sqrt{100+28}$=$\sqrt{128}$=8$\sqrt{2}$，
∴几何体外接球的半径为4$\sqrt{2}$，
∴几何体外接球的表面积为$4π•（4\sqrt{2}）^{2}$=128π．
故选：C．

点评 本题考查几何体外接球的表面积，考查基本不等式求最值，利用基本不等式求xy最大时x=y=8，是解答本题的关键．

练习册系列答案
相关题目
15．已知集合A={x|x2≥1}，B={x|y=$\sqrt{1-lo{g}_{2}x}$}，则A∩B=（　　）
A．（-∞，1]∪（1，2）B．（-∞，1]∪（2，+∞）C．（0，2]D．[1，2]
16．下列命题中正确的个数是（　　）
 ①命题“任意x∈（0，+∞），2x＞1”的否定是“任意x∉（0，+∞），2x≤1；
 ②命题“若cosx=cosy，则x=y”的逆否命题是真命题；
 ③若命题p为真，命题￢q为真，则命题p且q为真；
 ④命题“若x=3，则x2-2x-3=0”的否命题是“若x≠3，则x2-2x-3≠0”．
A．1个B．2个C．3个D．4个
13．方程x2+y2-2y=0所表示的曲线的特征是（　　）
A．关于直线y=x对称B．关于原点对称C．关于x轴对称D．关于y轴对称
20．直线$l：y=k（x-\frac{5}{2}）+\frac{3}{2}$被圆x2+y2-5x=0所截得的n条弦的长度成等差数列，最小弦长为数列的首项a1，最大弦长为an，若公差$d∈[{\frac{1}{7}，\frac{1}{5}}]$，则n的最大取值为（　　）
A．6B．7C．8D．9
10．已知双曲线$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{2}$=1，其双曲线的右焦点与抛物线y2=4$\sqrt{3}$x的焦点重合，则该双曲线的方程为${x}^{2}-\frac{{y}^{2}}{2}$=1．
17．已知函数$f（x）=\frac{1}{2}a{x^2}+3lnx，g（x）=-bx$，其中a，b∈R．设h（x）=f（x）-g（x），若$f'（\frac{{\sqrt{2}}}{2}）=0$，且f′（1）=g（-1）-2．
（1）求a，b的值；
（2）求函数h（x）的图象在点（1，-4）处的切线方程．
14．已知函数f（x）=（log${\;}_{\frac{1}{4}}$x）2-log${\;}_{\frac{1}{4}}$x+5，x∈[1，4]，求f（x）的最大值和最小值及对应的x值．
15．某几何体的三视图如图所示，其中俯视图是半径为4的圆面的四分之一，则该几何体的体积为16π．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网