题目内容
19．已知x，y满足不等式组$\left\{\begin{array}{l}{x-y+1≥0}\\{x+y-1≥0}\\{3x-y≤0}\end{array}\right.$，则目标函数z=2x-y的最小值为-1．分析 由约束条件作出可行域，化目标函数为直线方程的斜截式，数形结合得到最优解，把最优解的坐标代入目标函数得答案．
解答 解：由约束条件$\left\{\begin{array}{l}{x-y+1≥0}\\{x+y-1≥0}\\{3x-y≤0}\end{array}\right.$作出可行域如图，
化目标函数z=2x-y为y=2x-z，
由图可知，当直线y=2x-z过A（0，1）时，直线在y轴上的截距最大，z有最小值为-1．
故答案为：-1．
点评 本题考查简单的线性规划，考查了数形结合的解题思想方法，是中档题．
练习册系列答案
相关题目
8．
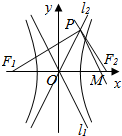已知F1，F2分别是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a，b＞0）的左、右焦点，l1，l2为双曲线的两条渐近线．设过点M（b，0）且平行于l1的直线交l2于点P．若PF1⊥PF2，则该双曲线的离心率为（ ）
已知F1，F2分别是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a，b＞0）的左、右焦点，l1，l2为双曲线的两条渐近线．设过点M（b，0）且平行于l1的直线交l2于点P．若PF1⊥PF2，则该双曲线的离心率为（ ）| A． | $\sqrt{3}$ | B． | $\sqrt{5}$ | C． | $\frac{\sqrt{14-2\sqrt{41}}}{2}$ | D． | $\frac{\sqrt{14+2\sqrt{41}}}{2}$ |