题目内容
4.若sin2x>cos2x,则x的取值范围是(kπ+$\frac{π}{4}$,$\frac{3π}{4}$+kπ)(k∈Z).分析 sin2x>cos2x,化为cos2x<0,利用余弦函数的图象与性质即可得出.
解答 解:∵sin2x>cos2x,
∴cos2x<0,
∴2kπ+$\frac{π}{2}$<2x$<\frac{3π}{2}$+2kπ,
解得kπ+$\frac{π}{4}$<x<$\frac{3π}{4}$+kπ(k∈Z).
∴x的取值范围是(kπ+$\frac{π}{4}$,$\frac{3π}{4}$+kπ)(k∈Z).
故答案为:(kπ+$\frac{π}{4}$,$\frac{3π}{4}$+kπ)(k∈Z).
点评 本题考查了余弦函数的图象与性质、倍角公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
13.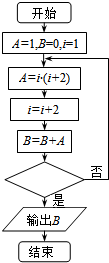 如图给出的是计算1×3+3×5+5×7+…+13×15的值的一个程序框图,其中判断框内应填入的条件不正确的是( )
如图给出的是计算1×3+3×5+5×7+…+13×15的值的一个程序框图,其中判断框内应填入的条件不正确的是( )
 如图给出的是计算1×3+3×5+5×7+…+13×15的值的一个程序框图,其中判断框内应填入的条件不正确的是( )
如图给出的是计算1×3+3×5+5×7+…+13×15的值的一个程序框图,其中判断框内应填入的条件不正确的是( )| A. | i≥13? | B. | i>14? | C. | i≥14? | D. | i≥15? |
 某几何体的三视图如图所示,其中俯视图是半径为4的圆面的四分之一,则该几何体的体积为16π.
某几何体的三视图如图所示,其中俯视图是半径为4的圆面的四分之一,则该几何体的体积为16π.