题目内容
5.已知一个等比数列首项为1,项数是偶数,其奇数项之和为85,偶数项之和为170,则这个数列的公比和项数分别为( )| A. | 8,2 | B. | 2,4 | C. | 4,10 | D. | 2,8 |
分析 假设等比数列项数为2n项,先根据偶数项的和与奇数项的和的比值,利用等比数列的性质求得数列的公比,进而根据奇数项的和,可求得n,从而可求等比数列的项数2n.
解答 解:设等比数列项数为2n项,所有奇数项之和为S奇,所有偶数项之和为S偶,
根据题意得:S奇=85,S偶=170,
∴q=$\frac{{S}_{偶}}{{S}_{奇}}$=2,又a1=1,
∴S奇=$\frac{{a}_{1}(1-{q}^{2n})}{1-{q}^{2}}$=85,整理得:1-4n=-3×85,即4n=256,
解得:n=4,
则这个等比数列的项数为8.
故选:D.
点评 本题主要以等比数列为载体,考查等比数列的性质,以及等比数列的求和公式,解题的关键是利用奇数项的和与偶数相的和求得数列的公比.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
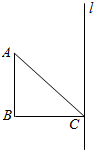 如图,三角形ABC是等腰直角三角形,∠B=90°,AB=1,直线l经过点C且与AB平行,将三角形ABC绕直线l旋转一周得到一个几何体.
如图,三角形ABC是等腰直角三角形,∠B=90°,AB=1,直线l经过点C且与AB平行,将三角形ABC绕直线l旋转一周得到一个几何体.