题目内容
1.已知等差数列{an}的前n项和 Sn,且a4=11,S8=100;数列{bn}满足${b_1}=\frac{1}{2}{a_1}$,anbn+1+bn+1=nbn.(1)求数列{an}的通项公式;
(2)求数列{bn}的前n项和Tn.
分析 (1)利用等差数列的通项公式与求和公式即可得出.
(2)利用等比数列的通项公式与求和公式即可得出.
解答 解:(1)设数列{an}的公差为d,由$\left\{\begin{array}{l}{a_4}={a_1}+3d=11\\{S_8}=8{a_1}+\frac{8×7}{2}d=100\end{array}\right.$,解得$\left\{\begin{array}{l}{a_1}=2\\ d=3\end{array}\right.$,
∴an=2+3(n-1)=3n-1.
(2)${b_1}=\frac{1}{2}{a_1}$=1,由anbn+1+bn+1=nbn可得:bn+1=$\frac{1}{3}$bn.
∴数列{bn}是等比数列,首项为1,公比为$\frac{1}{3}$.
故其前n项和${T_n}=\frac{{1-{{(\frac{1}{3})}^n}}}{{1-\frac{1}{3}}}=\frac{3}{2}-\frac{3}{2}{(\frac{1}{3})^n}$.
点评 本题考查了等差数列与等比数列的通项公式与求和公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
6.设θ为第二象限角,若tan(θ+$\frac{π}{4}$)=$\frac{1}{2}$,则sinθ+cosθ=( )
| A. | $-\frac{{\sqrt{10}}}{5}$ | B. | $\frac{{\sqrt{10}}}{5}$ | C. | $-\frac{{\sqrt{10}}}{10}$ | D. | $\frac{{\sqrt{10}}}{10}$ |
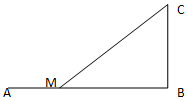 如图,设铁路AB长为50,BC⊥AB,且BC=10,为将货物从A运往C,现在AB上距点B为x的点M处修一公路至C,已知单位距离的铁路运费为2,公路运费为4.
如图,设铁路AB长为50,BC⊥AB,且BC=10,为将货物从A运往C,现在AB上距点B为x的点M处修一公路至C,已知单位距离的铁路运费为2,公路运费为4.