题目内容
过抛物线y2=2px（p＞0）的焦点作直线交抛物线于P（x1，y1）、Q（x2，y2）两点，若x1+x2=2，|PQ|=4，则抛物线方程是（ ）
| A、y2=4x |
| B、y2=8x |
| C、y2=2x |
| D、y2=6x |
考点：抛物线的标准方程
专题：计算题,圆锥曲线的定义、性质与方程
分析：利用抛物线的定义可得，|PQ|=|PF|+|QF|=x1+
+x2 +
，把x1+x2=2，|PQ|=4代入可得P值．
| p |
| 2 |
| p |
| 2 |
解答：
解：设抛物线y2=2px（p＞0）的焦点为F，
由抛物线的定义可知，
|PQ|=|PF|+|QF|=x1+
+x2 +
=（x1+x2）+p=2+p，
又|PQ|=4，∴p=2，
∴抛物线方程为y2=4x．
故选：A．
由抛物线的定义可知，
|PQ|=|PF|+|QF|=x1+
| p |
| 2 |
| p |
| 2 |
又|PQ|=4，∴p=2，
∴抛物线方程为y2=4x．
故选：A．
点评：本题考查抛物线的定义、标准方程，以及简单性质的应用，利用抛物线的定义是解题的关键．
练习册系列答案
相关题目
复数z=3+
，则
等于（ ）
| 3+4i |
| 4-3i |
. |
| z |
| A、3+i | B、3-i |
| C、4+i | D、4-i |
已知圆C：（x-l）2+y2=l与直线l：x-2y+1=0相交于A、B两点，则|AB|=（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
如图所示，程序框图（算法流程图）的输出值s=（ ）
| A、-1 | B、0 | C、1 | D、3 |
不等式（
） x2+ax＜（
）2x+a-2恒成立，则a的取值范围是（ ）
| 1 |
| 2 |
| 1 |
| 2 |
| A、[-2，2] |
| B、（-2，2） |
| C、[0，2] |
| D、[-3，3] |
“x＞3”是“x2＞9”的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、既充分又必要条件 |
| D、既不充分又不必要条件 |
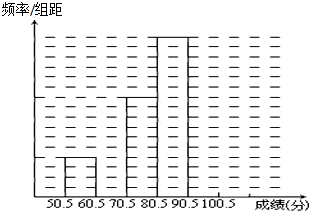某中学举行了一次“环保知识竞赛”，共有800名学生参加了这次竞赛．从中抽取了部分学生的成绩进行统计．请你根据尚未完成并有局部污损的频率分布表和频率分布直方图，解答下列问题：