题目内容
15．
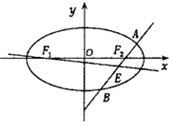已知椭圆C的方程为$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0），双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的一条渐近线与x轴所成的夹角为30°，且双曲线的焦距为4$\sqrt{2}$．（1）求椭圆C的方程；
（2）设F1，F2分别为椭圆C的左，右焦点，过F2作直线l（与x轴不重合）交于椭圆于A，B两点，线段AB的中点为E，记直线F1E的斜率为k，求k的取值范围．
分析 （1）由双曲线的渐近线方程及斜率公式，即可求得a2=3b2，c=2$\sqrt{2}$，即a2+b2=8，即可求得a和b的值，求得椭圆方程；
（2）设直线AB的方程，代入椭圆方程，利用韦达定理求得斜率丨k丨用t表示，利用基本不等式即可求得k的取值范围．
解答 解：（1）由一条渐近线与x轴所成的夹角为30°，则$\frac{b}{a}$=tan30°=$\frac{\sqrt{3}}{3}$，即a2=3b2，
由2c=4$\sqrt{2}$．c=2$\sqrt{2}$，则a2+b2=8，
解得：a2=8，b2=2，
∴椭圆的标准方程：$\frac{{x}^{2}}{6}+\frac{{y}^{2}}{2}=1$；
（2）由（1）可知：F2（2，0），直线AB的方程：x=ty+2，A（x1，y1），B（x2，y2），
$\left\{\begin{array}{l}{x=ty+2}\\{\frac{{x}^{2}}{6}+\frac{{y}^{2}}{2}=1}\end{array}\right.$，整理得：（t2+3）y2+4ty-2=0，
y1+y2=-$\frac{4t}{{t}^{2}+3}$，x1+x2=$\frac{12}{{t}^{2}+3}$，
则E（$\frac{6}{{t}^{2}+3}$，-$\frac{2t}{{t}^{2}+3}$），
由F1（-2，0），则直线F1E的斜率k=$\frac{\frac{2t}{{t}^{2}+3}}{-2-\frac{6}{{t}^{2}+3}}$=-$\frac{t}{{t}^{2}+6}$，
①当t=0时，k=0，
②当t≠0时，丨k丨=$\frac{丨t丨}{丨t{丨}^{2}+6}$=$\frac{1}{丨t丨+\frac{6}{丨t丨}}$≤$\frac{1}{2\sqrt{6}}$，
即丨k丨∈（0，$\frac{\sqrt{6}}{12}$]，
∴k的取值范围[-$\frac{\sqrt{6}}{12}$，$\frac{\sqrt{6}}{12}$]．
点评 本题考查椭圆的标准方程，直线与椭圆的位置关系，考查韦达定理，直线的斜率公式及基本不等式的应用，考查计算能力，属于中档题．
| A． | $\frac{3π}{4}$ | B． | $\frac{π}{4}$ | C． | $\frac{2π}{3}$ | D． | $\frac{5π}{6}$ |
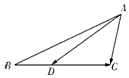如图，在△ABC中，∠BAC=60°，AB=2，AC=1，D是BC边上一点，且$\overrightarrow{CD}$=2$\overrightarrow{DB}$，则$\overrightarrow{AD}$•$\overrightarrow{BC}$ 的值为-2．| 单价x（元） | 8 | 8.2 | 8.4 | 8.6 | 8.8 | 9 |
| 销量y（件） | 90 | 84 | 83 | 80 | 75 | 68 |