题目内容
已知a
+b
=1,则以下成立的是( )
| 1-b2 |
| 1-a2 |
| A、a2+b2>1 |
| B、a2+b2=1 |
| C、a2+b2<1 |
| D、a2b2=1 |
考点:二维形式的柯西不等式
专题:不等式的解法及应用
分析:利用柯西不等式即可得出.
解答:
解:由柯西不等式,得1=a
+b
≤[a2+(1-a2)][(1-b2)+b2]=1,
当且仅当
=
时,上式取等号,
∴ab=
,化为a2b2=(1-a2)(1-b2),
于是 a2+b2=1.
故选:B.
| 1-b2 |
| 1-a2 |
当且仅当
| b | ||
|
| ||
| a |
∴ab=
| 1-a2 |
| 1-b2 |
于是 a2+b2=1.
故选:B.
点评:本题考查了柯西不等式的应用,属于基础题.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案
相关题目
一个平面将一个半径为2的实心球截为两个部分,且截面经过球心,那么每个部分的表面积为( )
| A、12π | B、16π |
| C、4π | D、8π |
用数学归纳法证明2n>n2(n∈N*,n≥5)成立时,第二步归纳假设正确写法( )
| A、假设n=k时命题成立 |
| B、假设n=k(k∈N*)时命题成立 |
| C、假设n=k(n≥5)时命题成立 |
| D、假设n=k(n>5)时命题成立 |
若P=
+
,Q=
+
(a≥0),则P,Q的大小关系为( )
| a+2 |
| a+5 |
| a+3 |
| a+4 |
| A、P>Q | B、P=Q |
| C、P<Q | D、由a的取值确定 |
若函数f(x)=
(a,b,c,d∈R)的图象如图所示,则a:b:c:d=( )
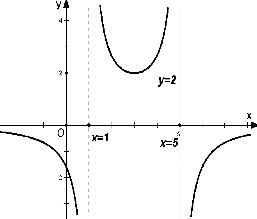
| d |
| ax2+bx+c |

| A、1:6:5:8 |
| B、1:6:5:(-8) |
| C、1:(-6):5:8 |
| D、1:(-6):5:(-8) |
已知数列{an}的前n项和为Sn,且Sn=n2+2n+1,则a3+a4+a5=( )
| A、11 | B、16 | C、27 | D、32 |
设直线y=t与函数f(x)=x
,g(x)=ex的图象分别交于点M,N,则当|MN|达到最小时t的值为( )
| 1 |
| 2 |
| A、1 | ||||
B、
| ||||
C、
| ||||
D、
|