题目内容
设直线y=t与函数f(x)=x
,g(x)=ex的图象分别交于点M,N,则当|MN|达到最小时t的值为( )
| 1 |
| 2 |
| A、1 | ||||
B、
| ||||
C、
| ||||
D、
|
考点:指数函数的定义、解析式、定义域和值域
专题:转化思想,函数的性质及应用,导数的概念及应用
分析:根据题意,求出f(x)的反函数f-1(x),g(x)的反函数g-1(x);
构造函数h(x)=f-1(x)-g-1(x),利用导数求出h(x)取得最小值,即|MN|达到最小值时x(即t)的值.
构造函数h(x)=f-1(x)-g-1(x),利用导数求出h(x)取得最小值,即|MN|达到最小值时x(即t)的值.
解答:
解:根据题意,∵f(x)=x
,∴f-1(x)=x2(x≥0);
∵g(x)=ex,∴g-1(x)=lnx(x≥0);
设h(x)=f-1(x)-g-1(x)=x2-lnx(x≥0),
∴h′(x)=2x-
=
;
令h′(x)=0,解得x=
;
∴x>
时,h′(x)>0,h(x)是增函数,0<x<
时,h′(x)<0,h(x)是减函数;
∴x=
时,h(x)取得最小值,即|MN|达到最小值,此时t=
.
故选:D.
| 1 |
| 2 |
∵g(x)=ex,∴g-1(x)=lnx(x≥0);
设h(x)=f-1(x)-g-1(x)=x2-lnx(x≥0),
∴h′(x)=2x-
| 1 |
| x |
| 2x2-1 |
| x |
令h′(x)=0,解得x=
| ||
| 2 |
∴x>
| ||
| 2 |
| ||
| 2 |
∴x=
| ||
| 2 |
| ||
| 2 |
故选:D.
点评:本题考查了求函数最值的问题,通常利用导数来研究函数的最值,解题的关键是构造函数,确定函数的单调性,从而求出函数的最值,是中档题.

练习册系列答案
相关题目
已知a
+b
=1,则以下成立的是( )
| 1-b2 |
| 1-a2 |
| A、a2+b2>1 |
| B、a2+b2=1 |
| C、a2+b2<1 |
| D、a2b2=1 |
如图,可作为函数y=f(x)的图象是( )
A、 |
B、 |
C、 |
D、 |
设函数f(x)=
,若关于x的方程f2(x)+bf(x)+c=0有且仅有三个不同的实数根x1、x2、x3,且x1<x2<x3,则x12+2x22+3x32等于( )
|
| A、6 | ||
| B、13 | ||
C、
| ||
D、
|
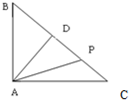 如图,已知△ABC中,AB=3,AC=4,BC=5,AD⊥BC于D点,点P为BC边所在直线上的一个动点,则
如图,已知△ABC中,AB=3,AC=4,BC=5,AD⊥BC于D点,点P为BC边所在直线上的一个动点,则| AP |
| AD |
| A、最大值为9 | ||
B、为定值
| ||
| C、最小值为3 | ||
| D、与P的位置有关 |
一个口袋中装有m个白球,n个黑球,从口袋中每次拿一个球不放回,第k次拿到黑球的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
已知f(x)是定义在R上的偶函数,且在(-∞,0)内是增函数,f(1)=0,若f(x)<0,则实数x的取值范围是( )
| A、(-1,0)∪(0,1) |
| B、(-∞,-1)∪(0,1) |
| C、(-1,0)∪(1,+∞) |
| D、(-∞,-1)∪(1,+∞) |
数列{an}中,a1=5,anan+1=2n,则
=( )
| a1 |
| a3 |
A、
| ||
| B、2 | ||
C、
| ||
D、
|