题目内容
若函数f(2x-1)的定义域为[-1,1],
(1)求函数f(1-3x)的定义域;
(2)求函数g(x)=f(x+
)f(x-
)的定义域;
(3)求函数h(x)=f(x+a)+f(x-a)(a>0)的定义域.
(1)求函数f(1-3x)的定义域;
(2)求函数g(x)=f(x+
| 1 |
| 4 |
| 1 |
| 4 |
(3)求函数h(x)=f(x+a)+f(x-a)(a>0)的定义域.
考点:函数的定义域及其求法,函数的值域
专题:函数的性质及应用
分析:(1)由题意知-3≤1-3x≤1,求出x的范围并用区间表示,是所求函数的定义域;
(2)由题意-3≤x≤1,根据x+
∈[-3,1],x-
∈[-3,1],得到x的范围,并用区间表示就是所求的定义域.
(3)由题意-3≤x≤1,根据x+a∈[-3,1],x-a∈[-3,1],得到x的范围,并用区间表示就是所求的定义域.
(2)由题意-3≤x≤1,根据x+
| 1 |
| 4 |
| 1 |
| 4 |
(3)由题意-3≤x≤1,根据x+a∈[-3,1],x-a∈[-3,1],得到x的范围,并用区间表示就是所求的定义域.
解答:
解:(1)∵函数f(2x-1)的定义域为[-1,1],
∴函数f(x)的定义域为[-3,1],
∴-3≤1-3x≤1,
∴0≤x≤
,
∴函数f(1-3x)的定义域[0,
];
(2)∵x+
∈[-3,1],x-
∈[-3,1],
解得-
≤x≤
,
∴函数g(x)=f(x+
)f(x-
)的定义域[-
,
];
(3)∵x+a∈[-3,1],x-a∈[-3,1],
∴
,
∵a>0,
当0<a<2时,即1-a>-3+a.
解得-3+a≤x≤1-a,
当a≥2时,无解
∴当0<a<2时,函数h(x)的定义域[-3+a,1-a].
当a≥2时,函数h(x)的定义域为空集.
∴函数f(x)的定义域为[-3,1],
∴-3≤1-3x≤1,
∴0≤x≤
| 4 |
| 3 |
∴函数f(1-3x)的定义域[0,
| 4 |
| 3 |
(2)∵x+
| 1 |
| 4 |
| 1 |
| 4 |
解得-
| 11 |
| 3 |
| 3 |
| 4 |
∴函数g(x)=f(x+
| 1 |
| 4 |
| 1 |
| 4 |
| 11 |
| 3 |
| 3 |
| 4 |
(3)∵x+a∈[-3,1],x-a∈[-3,1],
∴
|
∵a>0,
当0<a<2时,即1-a>-3+a.
解得-3+a≤x≤1-a,
当a≥2时,无解
∴当0<a<2时,函数h(x)的定义域[-3+a,1-a].
当a≥2时,函数h(x)的定义域为空集.
点评:本题重点考查了函数的定义域,复合函数的定义域问题,属于中档题.

练习册系列答案
相关题目
log28+log327+log525=( )
| A、5 | B、6 | C、7 | D、8 |
sin(-
π)的值等于( )
| 14 |
| 3 |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
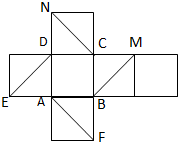 如图,为正方体的平面展开图,在这个正方体中
如图,为正方体的平面展开图,在这个正方体中