题目内容
5.在△ABC中,已知$\sqrt{3}asinC-c({2+cosA})=0$,其中角A、B、C所对的边分别为a、b、c.求(1)求角A的大小;
(2)若$a=\sqrt{6}$,△ABC的面积为$\frac{{\sqrt{3}}}{2}$,求sinB+sinC的值.
分析 (1)由正弦定理,得$\sqrt{3}sinAsinC-sinC({2+cosA})=0$,从而$\sqrt{3}sinA-cosA=2$,由此能求出角A.
(2)由$S=\frac{1}{2}bc{sinA}=\frac{{\sqrt{3}}}{2}$,得bc=2,由$a=\sqrt{6}$及余弦定理得$b+c=2\sqrt{2}$,由此能求出sinB+sinC的值.
解答 解:(1)∵在△ABC中,$\sqrt{3}asinC-c({2+cosA})=0$,
∴由正弦定理,得$\sqrt{3}sinAsinC-sinC({2+cosA})=0$,
∵sinC≠0,∴$\sqrt{3}sinA-cosA=2$.即$sin({A-\frac{π}{6}})=1$,而A∈(0,π)
∴$A-\frac{π}{6}=\frac{π}{2}$,则 $A=\frac{2π}{3}$------(6分)
(2)由$S=\frac{1}{2}bc{sinA}=\frac{{\sqrt{3}}}{2}$,得bc=2,
由$a=\sqrt{6}$及余弦定理得${({\sqrt{6}})^2}={b^2}+{c^2}-2bc{cosA}={b^2}+{c^2}+bc={({b+c})^2}-bc$,
即$b+c=2\sqrt{2}$,所以${sinB}+sinC=\frac{sinA}{a}({b+c})=1$.----(12分)
点评 本题考查角的大小、两角正弦值的和的求法,考查正弦定理、余弦定理、三角形面积公式、三角函数恒等式等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、函数与方程思想,是中档题.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
10.已知函数f(x)=x+$\frac{1}{x-1}$(x>1),则( )
| A. | f(x)的最大值为2 | B. | f(x)的最大值为3 | C. | f(x)的最小值为2 | D. | f(x)的最小值为3 |
20. 有一塔形几何体由若干个正方体构成,构成方式如图所示,上层正方体下底面的四个顶点是下层正方体上底面各边的中点.已知最底层正方体的棱长为2,且该塔形的表面积(含最底层正方体的底面面积)超过38,则该塔形中正方体的个数至少是( )
有一塔形几何体由若干个正方体构成,构成方式如图所示,上层正方体下底面的四个顶点是下层正方体上底面各边的中点.已知最底层正方体的棱长为2,且该塔形的表面积(含最底层正方体的底面面积)超过38,则该塔形中正方体的个数至少是( )
 有一塔形几何体由若干个正方体构成,构成方式如图所示,上层正方体下底面的四个顶点是下层正方体上底面各边的中点.已知最底层正方体的棱长为2,且该塔形的表面积(含最底层正方体的底面面积)超过38,则该塔形中正方体的个数至少是( )
有一塔形几何体由若干个正方体构成,构成方式如图所示,上层正方体下底面的四个顶点是下层正方体上底面各边的中点.已知最底层正方体的棱长为2,且该塔形的表面积(含最底层正方体的底面面积)超过38,则该塔形中正方体的个数至少是( )| A. | 4个 | B. | 5个 | C. | 6个 | D. | 7个 |
14.“sinαcosβ+cosαsinβ=$\frac{1}{2}$”是“$α+β=2kπ+\frac{π}{6}$,k∈Z”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
15.设集合U={-2,-1,0,1,2},A={x|x2-x-2=0},则∁UA=( )
| A. | {-2,1} | B. | {-1,2} | C. | {-2,0,1} | D. | {2,-1,0} |
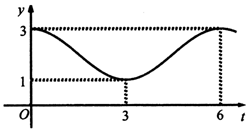 某工厂有甲、乙两生产车间,其污水瞬时排放量y(单位:m3/h )关于时间t(单位:h)的关系均近似地满足函数y=Asin(ωt+φ)+b(A>0,ω>0,0<φ<π),其图象如下:
某工厂有甲、乙两生产车间,其污水瞬时排放量y(单位:m3/h )关于时间t(单位:h)的关系均近似地满足函数y=Asin(ωt+φ)+b(A>0,ω>0,0<φ<π),其图象如下: