题目内容
设定义在R上的奇函数f(x)在(0,+∞)上为增函数,且f(2)=0,则不等式f(x)<0的解集为 .
考点:函数奇偶性的性质,函数单调性的性质
专题:函数的性质及应用
分析:利用奇函数的对称性、单调性即可得出.
解答:
解:如图所示,
不等式f(x)<0的解集为
(-∞,-2)∪(0,2).
故答案为:(-∞,-2)∪(0,2).

不等式f(x)<0的解集为
(-∞,-2)∪(0,2).
故答案为:(-∞,-2)∪(0,2).
点评:本题考查了奇函数的对称性、单调性,属于基础题.

练习册系列答案
相关题目
已知椭圆的长轴在y轴上,其椭圆方程为:
+
=1,且焦距为4,则m等于( )
| x2 |
| m |
| y2 |
| 13 |
| A、4 | B、5 | C、7 | D、9 |
函数y=loga(2x-3)+2的图象恒过定点P,P在指数函数f(x)的图象上,则f(-1)的值为( )
A、
| ||||
B、
| ||||
C、-
| ||||
D、-
|
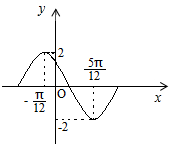 如图是函数y=Asin(ωx+φ)在一个周期内的图象,如果A>0,ω>0,0<φ<π,则此函数的解析式为
如图是函数y=Asin(ωx+φ)在一个周期内的图象,如果A>0,ω>0,0<φ<π,则此函数的解析式为