题目内容
已知f(x)=
,求:f(-5)+f(-4)+f(-3)+…+f(6)= .
| 1 | ||
2x+
|
考点:函数的值
专题:函数的性质及应用
分析:f(x)+f(1-x)=
,设S=f(-5)+f(-4)+f(-3)+…+f(6),则S=f(6)+f(5)+…+f(-4)+f(-5),两式相加,求出2S=6
,由此能求出S=3
.
| ||
| 2 |
| 2 |
| 2 |
解答:
解:f(x)+f(1-x)=
+
=
=
,
设S=f(-5)+f(-4)+f(-3)+…+f(6),
则S=f(6)+f(5)+…+f(-4)+f(-5),
两式相加,
2S=[f(-5)+f(6)]+[f(-4)+f(5)]+…+[f(6)+f(-5)]
=
×12=6
,
∴S=3
.
故答案为:3
.
| 1 | ||
2x+
|
| 1 | ||
21-x+
|
=
2
| ||
4+
|
| ||
| 2 |
设S=f(-5)+f(-4)+f(-3)+…+f(6),
则S=f(6)+f(5)+…+f(-4)+f(-5),
两式相加,
2S=[f(-5)+f(6)]+[f(-4)+f(5)]+…+[f(6)+f(-5)]
=
| ||
| 2 |
| 2 |
∴S=3
| 2 |
故答案为:3
| 2 |
点评:本题考查函数值的求法,是基础题,解题时要认真审题,注意倒序相加法的合理运用.

练习册系列答案
相关题目
△ABC的外接圆半径为1,圆心为O,且3
+4
+5
=
,则
在
上的投影为( )
| OA |
| OB |
| OC |
| 0 |
| OC |
| AB |
A、-
| ||||
B、
| ||||
C、-
| ||||
D、
|
已知椭圆的长轴在y轴上,其椭圆方程为:
+
=1,且焦距为4,则m等于( )
| x2 |
| m |
| y2 |
| 13 |
| A、4 | B、5 | C、7 | D、9 |
已知函数f(x)=
(et-e-t)dt,则不等式f(loga2)+f(loga
)≤2f(1)的解集为( )
| ∫ | x 0 |
| 1 |
| 2 |
A、(0,
| ||
| B、[2,+∞) | ||
C、[
| ||
D、(0,
|
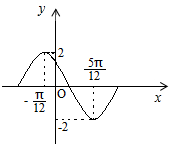 如图是函数y=Asin(ωx+φ)在一个周期内的图象,如果A>0,ω>0,0<φ<π,则此函数的解析式为
如图是函数y=Asin(ωx+φ)在一个周期内的图象,如果A>0,ω>0,0<φ<π,则此函数的解析式为