题目内容
有20件产品,其中6件是次品,其余都是合格品,现不放回地从中依次抽2件,求:
(1)第一次抽到次品的概率;
(2)第一次和第二次都抽到次品的概率;
(3)在第一次抽到次品的条件下,第二次抽到次品的概率.
(1)第一次抽到次品的概率;
(2)第一次和第二次都抽到次品的概率;
(3)在第一次抽到次品的条件下,第二次抽到次品的概率.
考点:古典概型及其概率计算公式
专题:概率与统计
分析:(1)因为有6件是次品,第一次抽到次品,有6中可能,产品共有20件,不考虑限制,任意抽一件,有20中可能,所以概率为两者相除.
(2)因为是不放回的从中依次抽取2件,所以第一次抽到次品有6种可能,第二次抽到次品有5种可能,第一次和第二次都抽到次品有5×6种可能,总情况是先从20件中任抽一件,再从剩下的19件中任抽一件,所以有20×19种可能,再令两者相除即可.
(3)因为第一次抽到次品,所以剩下的19件中有5件次品,所以,抽到次品的概率为
.
(2)因为是不放回的从中依次抽取2件,所以第一次抽到次品有6种可能,第二次抽到次品有5种可能,第一次和第二次都抽到次品有5×6种可能,总情况是先从20件中任抽一件,再从剩下的19件中任抽一件,所以有20×19种可能,再令两者相除即可.
(3)因为第一次抽到次品,所以剩下的19件中有5件次品,所以,抽到次品的概率为
| 5 |
| 19 |
解答:
解:设“第一次抽到次品”为事件A,“第二次都抽到次品”为事件B,事件A和事件B相互独立.
依题意得:
(1)第一次抽到次品的概率为P(A)=
=
;
(2)第一次和第二次都抽到次品的概率为P(AB)=
=
;
(3)在第一次抽到次品的条件下,第二次抽到次品的概率为:P(B|A)=
=
÷
=
.
依题意得:
(1)第一次抽到次品的概率为P(A)=
| 6 |
| 20 |
| 3 |
| 10 |
(2)第一次和第二次都抽到次品的概率为P(AB)=
| 5×6 |
| 20×19 |
| 3 |
| 38 |
(3)在第一次抽到次品的条件下,第二次抽到次品的概率为:P(B|A)=
| P(AB) |
| P(A) |
| 1 |
| 19 |
| 1 |
| 5 |
| 5 |
| 19 |
点评:本题考查了有条件的概率的求法,做题时要认真分析,找到正确方法.

练习册系列答案
相关题目
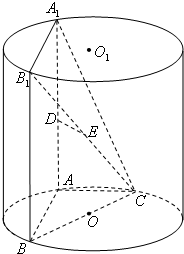 如图,AA1,BB1为圆柱OO1的母线,BC是底面圆O的直径,D,E分别是AA1,CB1的中点,DE⊥面CBB1.
如图,AA1,BB1为圆柱OO1的母线,BC是底面圆O的直径,D,E分别是AA1,CB1的中点,DE⊥面CBB1.