题目内容
20.已知定义在R上的奇函数f(x)=$\frac{a}{{2}^{x}+1}$+b的图象过点(-1,$\frac{1}{3}$),则f(2)=-$\frac{3}{5}$.分析 根据函数的奇偶性以及f(-1)=$\frac{1}{3}$,求出a,b的值,从而求出f(x)的表达式,得到f(2)的值即可.
解答 解:∵函数f(x)是奇函数,
∴f(-x)=$\frac{a}{{2}^{-x}+1}$+b=$\frac{(a+b{)2}^{x}+b}{{2}^{x}+1}$=-f(x)=$\frac{-{b2}^{x}-a-b}{{2}^{x}+1}$,
∴a+b=-b,b=-a-b,即a+2b=0①,
而f(-1)=$\frac{2}{3}$a+b=$\frac{1}{3}$②,
由①②解得:a=2,b=-1,
∴f(x)=$\frac{2}{{2}^{x}+1}$-1,
∴f(2)=-$\frac{3}{5}$,
故答案为:-$\frac{3}{5}$.
点评 本题考查了函数的奇偶性问题,考查求函数的解析式问题,是一道基础题.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
8.将红、黄、蓝、黑四只铅笔分给三名同学,每名同学至少分到一支铅笔,且红、黄两只铅笔不能分给同一名同学,则不同的分法种数为( )
| A. | 12 | B. | 20 | C. | 30 | D. | 42 |
3.在平面直角坐标系xOy中,已知点A(4,3),点B是圆(x+1)2+y2=4上的动点,则线段AB的中点M的轨迹方程是( )
| A. | ${(x-\frac{3}{2})^2}+{(y-\frac{3}{2})^2}=1$ | B. | ${(x-\frac{3}{2})^2}+{(y-\frac{3}{2})^2}=4$ | C. | (x-3)2+(y-3)2=1 | D. | (x-3)2+(y-3)2=2 |
4.下列选项错误的是( )
| A. | 命题“若x≠1,则x2-3x+2≠0”的逆否命题是“若x2-3x+2=0,则x=1” | |
| B. | “x>2”是“x2-3x+2>0”的充分不必要条件 | |
| C. | 若命题“p:?x∈R,x2+x+1≠0”,则“¬p:?x0∈R,x02+x0+1=0” | |
| D. | 若“p∨q”为真命题,则p、q均为真命题 |
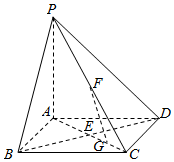 如图,四棱锥P-ABCD的底面是正方形,侧棱PA⊥面ABCD,BD交AC于点E,F是PC中点,G为AC上一动点.
如图,四棱锥P-ABCD的底面是正方形,侧棱PA⊥面ABCD,BD交AC于点E,F是PC中点,G为AC上一动点.