题目内容
15．已知点A（1，3），B（-2，-1），若直线l：y=k（x-2）+1与线段AB相交，则k的取值范围（ ）| A． | k≥$\frac{1}{2}$ | B． | k≤-2 | C． | k≥$\frac{1}{2}$或k≤-2 | D． | -2≤k≤$\frac{1}{2}$ |
分析 直线l：y=k（x-2）+1经过定点P（2，1），利用斜率计算公式可得：kPA，kPB，根据直线l：y=k（x-2）+1与线段AB相交，即可得出．
解答 解：直线l：y=k（x-2）+1经过定点P（2，1），
∵kPA=$\frac{3-1}{1-2}$=-2，kPB=$\frac{-1-1}{-2-2}$=$\frac{1}{2}$，
又直线l：y=k（x-2）+1与线段AB相交，
∴-2≤k$≤\frac{1}{2}$，
故选：D．
点评 本题考查了直线的倾斜角与斜率的关系，考查了数形结合方法、计算能力，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
5．已知函数$y={log_a}（{x^2}-ax+\frac{1}{2}）$，对任意的x1，x2∈[1，+∞），且x1≠x2时，满足$\frac{{f（{x_2}）-f（{x_1}）}}{{{x_2}-{x_1}}}＞0$，则实数a的取值范围是（ ）
| A． | $（1，\frac{3}{2}）$ | B． | $（{\frac{3}{2}，+∞}]$ | C． | （1，2] | D． | [2，+∞） |
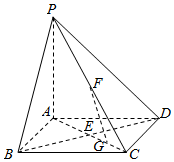如图，四棱锥P-ABCD的底面是正方形，侧棱PA⊥面ABCD，BD交AC于点E，F是PC中点，G为AC上一动点．
4．两圆C1：x2+y2=4与C2：x2+y2-2x-1=0的位置关系是（ ）
| A． | 相外切 | B． | 相内切 | C． | 相交 | D． | 外离 |