题目内容
20.在△ABC中,角A,B,C的对边分别是a,b,c,且满足a2+b2=2c2,sinAcosB=2cosAsinB.(Ⅰ)求cosC的值;
(Ⅱ)若$c=\sqrt{6}$,求△ABC的面积.
分析 (I)利用余弦定理即可得出;
(II)利用(I)、三角形面积计算公式即可得出.
解答 解:(Ⅰ)∵sinAcosB=2cosAsinB,
∴$a×\frac{{{a^2}+{c^2}-{b^2}}}{2ac}=2b×\frac{{{b^2}+{c^2}-{a^2}}}{2bc}$
化简得:${a^2}-{b^2}=\frac{1}{3}{c^2}$,
联立$\left\{\begin{array}{l}{a^2}-{b^2}=\frac{1}{3}{c^2}\\{a^2}+{b^2}=2{c^2}\end{array}\right.$,得$\left\{\begin{array}{l}{a^2}=\frac{7}{6}{c^2}\\{b^2}=\frac{5}{6}{c^2}\end{array}\right.$(4分)
∴$cosC=\frac{{{a^2}+{b^2}-{c^2}}}{2ab}=\frac{c^2}{{2\sqrt{\frac{7}{6}}c•\sqrt{\frac{5}{6}}c}}=\frac{{3\sqrt{35}}}{35}$(8分)
(Ⅱ)由$c=\sqrt{6}$,
可得:$a=\sqrt{7},b=\sqrt{5}$,$sinC=\sqrt{1-{{cos}^2}C}=\frac{{\sqrt{26}}}{{\sqrt{35}}}$(12分)
$S=\frac{1}{2}absinC=\frac{1}{2}\sqrt{7}•\sqrt{5}•\frac{{\sqrt{26}}}{{\sqrt{35}}}=\frac{{\sqrt{26}}}{2}$(15分)
点评 本题考查了余弦定理、三角形面积计算公式、同角三角函数基本关系式,考查了推理能力与计算能力,属于中档题.

| A. | 60 | B. | 180 | C. | 240 | D. | 360 |
| A. | $(1,\frac{3}{2})$ | B. | $({\frac{3}{2},+∞}]$ | C. | (1,2] | D. | [2,+∞) |
| A. | ${A}_{5}^{2}$${A}_{2}^{2}$ | B. | ${A}_{7}^{7}$-${A}_{2}^{2}$${A}_{6}^{6}$ | ||
| C. | ${A}_{7}^{7}$-${A}_{6}^{6}$ | D. | ${C}_{10}^{8}$0.820.28 |
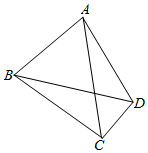 如图,在四边形ABCD中,AB=BD=$\sqrt{2}$,AC=$\sqrt{6}$,AD=2,∠ABC=120°.
如图,在四边形ABCD中,AB=BD=$\sqrt{2}$,AC=$\sqrt{6}$,AD=2,∠ABC=120°.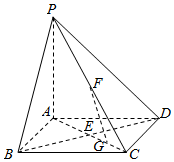 如图,四棱锥P-ABCD的底面是正方形,侧棱PA⊥面ABCD,BD交AC于点E,F是PC中点,G为AC上一动点.
如图,四棱锥P-ABCD的底面是正方形,侧棱PA⊥面ABCD,BD交AC于点E,F是PC中点,G为AC上一动点.