题目内容
在[0,2]上任取两数a,b,则函数f(x)=x2+
x+b有零点的概率为 .
| a |
考点:几何概型
专题:概率与统计
分析:函数f(x)=x2+
x+b有零点的条件,得到a,b满足的条件,利用几何概型的概率公式求出对应的面积即可得到结论.
| a |
解答:
解;∵a,b是区间[0,2]上的两个数,
∴a,b满足不等式
,对应区域面积为2×2=4,
若函数f(x)=x2+
x+b有零点,
则△=a-4b≥0,对应的区域为直线a-4b=0的下方,
作出对应的图象如图(阴影部分):
由
,解得
,即C(2,
),
则阴影部分的面积为
×2×
=
,
则根据几何概型的概率公式可得所求的概率为P=
=
,
故答案为:
.
∴a,b满足不等式
|

若函数f(x)=x2+
| a |
则△=a-4b≥0,对应的区域为直线a-4b=0的下方,
作出对应的图象如图(阴影部分):
由
|
|
| 1 |
| 2 |
则阴影部分的面积为
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
则根据几何概型的概率公式可得所求的概率为P=
| ||
| 4 |
| 1 |
| 8 |
故答案为:
| 1 |
| 8 |
点评:本题主要考查几何概型的概率计算,根据二次函数零点存在的条件求出a,b满足的条件是解决本题的关键.

练习册系列答案
相关题目
已知变量x,y满足约束条件
,若目标函数z=y+ax仅在点(5,3)处取得最小值,则实数a的取值范围为( )
|
| A、(-∞,-1) | ||
| B、(0,+∞) | ||
C、(
| ||
| D、(1,+∞) |
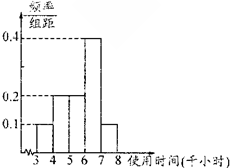 节能灯的质量通过其正常使用时间来衡量,使用时间越长,表明治疗越好.若使用时间小于4千小时的产品为不合格产品;使用时间在4千小时到6千小时(不含6千小时)的产品为合格品;使用时间大于或等于6千小时的产品为优质品.某节能灯生产厂家为了解同一类型号的某批次产品的质量情况,随机抽取了部分产品作为样本,得到实验结果的频率直方图如图所示.若上述实验结果中使用时间落入各组的频率作为相应的概率.
节能灯的质量通过其正常使用时间来衡量,使用时间越长,表明治疗越好.若使用时间小于4千小时的产品为不合格产品;使用时间在4千小时到6千小时(不含6千小时)的产品为合格品;使用时间大于或等于6千小时的产品为优质品.某节能灯生产厂家为了解同一类型号的某批次产品的质量情况,随机抽取了部分产品作为样本,得到实验结果的频率直方图如图所示.若上述实验结果中使用时间落入各组的频率作为相应的概率.