题目内容
19.在平面四边形ABCD中,∠B=∠D=$\frac{3}{4}$∠C=90°,BC=2,AD=3,则CD=3$\sqrt{3}$-4.分析 延长BC,AD交于点E,则∠E=30°,根据直角三角形的性质可用CD表示出其余各边,利用勾股定理列方程解出CD.
解答 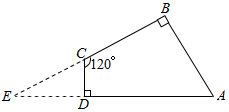 解:延长BC,AD,延长线交于点E.
解:延长BC,AD,延长线交于点E.
∵∠B=∠D=$\frac{3}{4}$∠C=90°,∴∠D=120,∠A=60°.∴∠E=30°.
设CD=x,则CE=2x,DE=$\sqrt{3}$x,∴AE=AD+DE=3+$\sqrt{3}$x,BE=BC+CE=2+2x.
∴AB=$\frac{1}{2}$AE=$\frac{3+\sqrt{3}x}{2}$.
∵tanE=$\frac{AB}{BE}$=$\frac{\sqrt{3}}{3}$,∴$\frac{\frac{3+\sqrt{3}x}{2}}{2+2x}=\frac{\sqrt{3}}{3}$,解得x=3$\sqrt{3}$-4.
故答案为3$\sqrt{3}$-4.
点评 本题考查了勾股定理,含30°角的直角三角形的性质,属于基础题.

练习册系列答案
相关题目