题目内容
3.设集合A=[-1,+∞),B=[t,+∞),对应法则f:x→y=x2,若能够建立从A到B的函数f:A→B,则实数t的取值范围是(-∞,0].分析 由题意得y≥0,利用B=[t,+∞),从而求出t的范围.
解答 解:∵集合A=[-1,+∞),f:x→y=x2,为A到B的映射
∴y≥0
∵B=[t,+∞),
∴t≤0.
故答案为:(-∞,0].
点评 本题考查的知识点是映射的定义,熟练掌握映射定义,本题属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.若集合A={1,2,3,4},B={2,4,7,8},则集合A∪B等于.( )
| A. | {1,2,3,4} | B. | {1,3,4} | C. | {1,2,3,8,4,7} | D. | {0,1,2,3,4,7,8} |
18.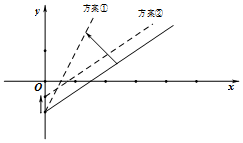 如图是某条公共汽车线路收支差额y与乘客量x的图象(实线),由于目前本线路亏损,公司有关人员提出两种扭亏为盈的方案(虚线),这两种方案分别是( )
如图是某条公共汽车线路收支差额y与乘客量x的图象(实线),由于目前本线路亏损,公司有关人员提出两种扭亏为盈的方案(虚线),这两种方案分别是( )
 如图是某条公共汽车线路收支差额y与乘客量x的图象(实线),由于目前本线路亏损,公司有关人员提出两种扭亏为盈的方案(虚线),这两种方案分别是( )
如图是某条公共汽车线路收支差额y与乘客量x的图象(实线),由于目前本线路亏损,公司有关人员提出两种扭亏为盈的方案(虚线),这两种方案分别是( )| A. | 方案①降低成本,票价不变,方案②提高票价而成本不变; | |
| B. | 方案①提高票价而成本不变,方案②降低成本,票价不变; | |
| C. | 方案①降低成本,票价提高,方案②提高票价而成本不变; | |
| D. | 方案①提高成本,票价不变,方案②降低票价且成本降低 |
15.已知a,b,c分别为△ABC三个内角A,B,C的对边,(sinA+sinB)(a-b)=(sinC-sinB)c,S△ABC=$\sqrt{3}$,c=4b,则函数f(x)=bx2-ax+c的零点个数为( )
| A. | 0 | B. | 1 | C. | 2 | D. | 不确定 |
13.设复数${z_1}=\frac{{\sqrt{3}}}{2}+\frac{1}{2}i$,z2=3+4i,其中i为虚数单位,则$\frac{{|z_1^{2016}|}}{{|{z_2}|}}$=( )
| A. | $\frac{2}{2015}$ | B. | $\frac{1}{2016}$ | C. | $\frac{1}{25}$ | D. | $\frac{1}{5}$ |