题目内容
13．设复数${z_1}=\frac{{\sqrt{3}}}{2}+\frac{1}{2}i$，z2=3+4i，其中i为虚数单位，则$\frac{{|z_1^{2016}|}}{{|{z_2}|}}$=（ ）| A． | $\frac{2}{2015}$ | B． | $\frac{1}{2016}$ | C． | $\frac{1}{25}$ | D． | $\frac{1}{5}$ |
分析 由已知求出${{z}_{1}}^{2016}$，在求出|z2|，代入$\frac{{|z_1^{2016}|}}{{|{z_2}|}}$得答案．
解答 解：∵${z_1}=\frac{{\sqrt{3}}}{2}+\frac{1}{2}i$，∴${{z}_{1}}^{2016}=[（\frac{\sqrt{3}}{2}+\frac{1}{2}i）^{3}]^{672}={i}^{672}=1$，
∵z2=3+4i，∴|z2|=5，
∴$\frac{{|z_1^{2016}|}}{{|{z_2}|}}$=$\frac{1}{5}$．
故选：D．
点评 本题考查复数代数形式的乘除运算，考查了复数的基本概念，是基础的计算题．
练习册系列答案
科学实验活动册系列答案
相关题目
5．
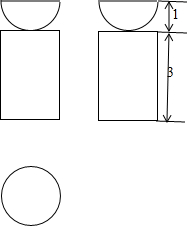如图是一个组合体的三视图，根据图中数据，可得该几何体的体积是（ ）
如图是一个组合体的三视图，根据图中数据，可得该几何体的体积是（ ）| A． | $\frac{38π}{3}$ | B． | $\frac{19π}{3}$ | C． | $\frac{13π}{3}$ | D． | $\frac{11π}{3}$ |
3．在△ABC中，$\overrightarrow{BD}$=$\frac{1}{2}$$\overrightarrow{DC}$，$\overrightarrow{AB}$=$\overrightarrow{a}$，$\overrightarrow{AC}$=$\overrightarrow{b}$，且则$\overrightarrow{AD}$=（ ）
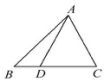
| A． | $\frac{4}{3}$$\overrightarrow{a}$-$\frac{1}{3}$$\overrightarrow{b}$ | B． | $\frac{2}{3}$$\overrightarrow{a}$+$\frac{1}{3}$$\overrightarrow{b}$ | C． | $\frac{1}{3}$$\overrightarrow{a}$-$\frac{4}{3}$$\overrightarrow{b}$ | D． | $\frac{1}{3}$$\overrightarrow{a}$+$\frac{2}{3}$$\overrightarrow{b}$ |