题目内容
15.定义域为R的函数f(x)是奇函数,当x≥0时,f(x)=|x-a2|-a2,且对x∈R,恒有f(x-3)≤f(x),则实数a的取值范围为[-$\frac{\sqrt{3}}{2}$,$\frac{\sqrt{3}}{2}$].分析 根据函数奇偶性的性质求出函数f(x)的解析式,讨论a的取值,作出函数f(x)的图象,利用图象平移以及数形结合进行求解即可.
解答 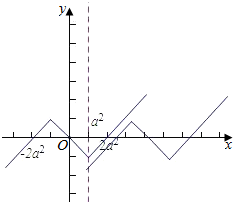 解:∵定义域为R的函数f(x)是奇函数,当x≥0时,f(x)=|x-a2|-a2,
解:∵定义域为R的函数f(x)是奇函数,当x≥0时,f(x)=|x-a2|-a2,
∴若x<0,则-x>0,
则f(-x)=|-x-a2|-a2=-f(x),
即f(x)=-|x+a2|+a2,x<0,
若a=0,则f(x)=x,为增函数,恒有f(x-3)≤f(x),成立,
当a≠0时,函数f(x)的图象如图:
∵f(x-3)的图象可以函数是由函数f(x)的图象向右平移3个单位得到的,
需要函数f(x)的图象至少向左平移2a2-(-2a2)=4a2个单位才能满足f(x-3)≤f(x),恒成立,
则4a2≤3,即-$\frac{\sqrt{3}}{2}$≤a≤$\frac{\sqrt{3}}{2}$,且a≠0,
综上-$\frac{\sqrt{3}}{2}$≤a≤$\frac{\sqrt{3}}{2}$,
故答案为:[-$\frac{\sqrt{3}}{2}$,$\frac{\sqrt{3}}{2}$]
点评 本题主要考查不等式恒成立问题,利用函数奇偶性求出函数的解析式,以及利用分类讨论和数形结合以及图象平移关系是解决本题的关键.综合性较强,难度较大.

练习册系列答案
 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
10.${∫}_{0}^{1}$1dx的值为( )
| A. | 0 | B. | 1 | C. | 2 | D. | $\frac{1}{2}$ |
7.一物体在力F(x)=3x2-2x+5(力单位:N,位移单位:m)作用下沿与力F(x)相同的方向由x=5m直线运动到x=10m所做的功是( )
| A. | 925J | B. | 850J | C. | 825J | D. | 800J |
2.若直线l1:(2m+1)x-4y+3m=0与直线l2:x+(m+5)y-3m=0平行,则m的值为( )
| A. | $-\frac{9}{2}或-1$ | B. | $-\frac{9}{2}$ | C. | $-\frac{19}{2}$ | D. | -1 |