题目内容
2.若直线l1:(2m+1)x-4y+3m=0与直线l2:x+(m+5)y-3m=0平行,则m的值为( )| A. | $-\frac{9}{2}或-1$ | B. | $-\frac{9}{2}$ | C. | $-\frac{19}{2}$ | D. | -1 |
分析 直线l1的斜率一定存在,所以,当两直线平行时,l2的斜率存在,求出l2的斜率,利用它们的斜率相等解出m的值.
解答 解:直线l1的斜率一定存在,为 $\frac{2m+1}{4}$,但当m=-5时,l2的斜率不存在,两直线不平行.
当m≠-5时,l2的斜率存在且等于$\frac{2m+1}{-4}$=$\frac{1}{m+5}$≠$\frac{3m}{-3m}$=-1,
解得m=-$\frac{9}{2}$,
故选:B.
点评 本题考查两直线平行的条件,两直线平行时,它们的斜率相等或者都不存在.

练习册系列答案
相关题目
12.在直三棱柱ABC-A1B1C1中,BC⊥AC,AC=12,BC=5,若一个球和它的各个面都相切,则该三棱柱的表面积为( )
| A. | 60 | B. | 180 | C. | 240 | D. | 360 |
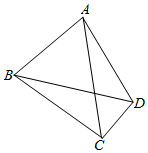 如图,在四边形ABCD中,AB=BD=$\sqrt{2}$,AC=$\sqrt{6}$,AD=2,∠ABC=120°.
如图,在四边形ABCD中,AB=BD=$\sqrt{2}$,AC=$\sqrt{6}$,AD=2,∠ABC=120°.