题目内容
3.设α∈(0,$\frac{π}{2}$),若cos(α+$\frac{π}{4}$)=$\frac{\sqrt{2}}{10}$,则sinα的值为$\frac{3}{5}$.分析 根据α的范围求出sin($α+\frac{π}{4}$),使用两角差的正弦函数公式计算.
解答 解:∵α∈(0,$\frac{π}{2}$),∴α+$\frac{π}{4}$∈($\frac{π}{4}$,$\frac{3π}{4}$),
∴sin($α+\frac{π}{4}$)=$\sqrt{1-co{s}^{2}(α+\frac{π}{4})}$=$\frac{7\sqrt{2}}{10}$.
∴sinα=sin[(α+$\frac{π}{4}$)-$\frac{π}{4}$]=sin($α+\frac{π}{4}$)cos$\frac{π}{4}$-cos($α+\frac{π}{4}$)sin$\frac{π}{4}$
=$\frac{7\sqrt{2}}{10}×\frac{\sqrt{2}}{2}-\frac{\sqrt{2}}{10}×\frac{\sqrt{2}}{2}$=$\frac{3}{5}$.
故答案为:$\frac{3}{5}$.
点评 本题考查了两角差的正弦函数公式,属于基础题.

练习册系列答案
相关题目
12.在直三棱柱ABC-A1B1C1中,BC⊥AC,AC=12,BC=5,若一个球和它的各个面都相切,则该三棱柱的表面积为( )
| A. | 60 | B. | 180 | C. | 240 | D. | 360 |
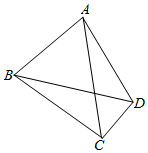 如图,在四边形ABCD中,AB=BD=$\sqrt{2}$,AC=$\sqrt{6}$,AD=2,∠ABC=120°.
如图,在四边形ABCD中,AB=BD=$\sqrt{2}$,AC=$\sqrt{6}$,AD=2,∠ABC=120°.