题目内容

已知向量
a
、
b
满足|
a
|=12，|
b
|=15，|
a
+
b
|=25，则|
a
-
b
|为
 
．
考点：平面向量数量积的运算,向量的模
专题：平面向量及应用
分析：由已知结合|
a
+
b
|2=(
a
+
b
)2求得2
a
•
b
，再由|
a
-
b
|=
(
a
-
b
)2
得答案．
解答： 解：(
a
+
b
)2=
a
2+2
a
•
b
+
b
2，
∵|
a
|=12，|
b
|=15，|
a
+
b
|=25，
∴252=122+2
a
•
b
+152，即2
a
•
b
=256．
∴|
a
-
b
|=
(
a
-
b
)2
=
a
2-2
a
•
b
+
b
2

=
122-256+152
=
113
．
故答案为：
113
．
点评：本题考查了平面向量的数量积运算，关键是对
a
2=|
a
|2的运用，是中档题．
练习册系列答案
相关题目
平面上定点F（0，1）和定直线l：y=-1，P为该平面上的动点，过P作直线l的垂线，垂足为Q，且(
PF
+
PQ
)•(
PF
-
PQ
)=0．
（1）求动点P的轨迹C的方程；
（2）过点F的直线交轨迹C于A、B两点，交直线l于点N，已知
NA
=λ1
AF
，
NB
=λ2
BF
，求证：λ1+λ2为定值．
如果等比数列{an}的首项、公比之和为1且首项是公比的2倍，那么它的前n项的和为（　　）
A、
1
2
（1-
1
3n
）
B、1-（
2
3
）n
C、1-
1
3n-1
D、1-
1
3n
记
.
a1a2a3…an
为一个n位正整数，其中a1，a2，…，an都是正整数，1≤a1≤9，0≤ai≤9（i=2，3，…，n）．若对任意的正整数j（1≤j≤n），至少存在另一个正整数k（1≤k≤n），使得aj=ak，则称这个数为“n位重复数”．根据上述定义，“四位重复数”的个数为．
 
．
已知数列{an}满足a1=10，an+1=
an-3，n＞3
-an+1，n≤3
．
（1）求数列{an}的前n项和Sn；
（2）已知自大到小的3个正数b1、b2、b3满足b1+b2+b3=21，b1b2+b2b3+b3b1=138，证明：当b3≥a3时，则有b1≥a1．
函数f（x）=5x，x∈（-2，4）是奇函数．
 
（判断对错）．
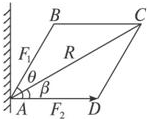如图所示，支座A受F1，F2两个力的作用，已知|F1|=45N，与水平线成θ角，|F2|=20N，沿水平方向，两个力的合力|F|=50N，求角θ以及合力F与水平线夹角的夹角β．
函数y=2x2的图象关于y轴对称．
 
（判断对错）．
如图，PA⊥平面ABCD，四边形ABCD为矩形，PA=AB=
3
，AD=1，点F是PB的中点，点E在边BC上移动．
（Ⅰ）当点E为BC的中点时，证明EF∥平面PAC；
（Ⅱ）求三棱锥E-PAD的体积；
（Ⅲ）证明：无论点E在边BC的何处，都有PE⊥AF．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网